고등수학 (2015 개정 교육과정)/수학2
[함수 개형] 위로 볼록, 아래로 볼록 수식으로 나타내기
한량 지아이
2023. 10. 1. 23:48
반응형
직선을 제외한 곡선 함수는 평면에서 위로 볼록하거나, 아래로 볼록하거나 둘 중 하나입니다.
그런데 보통 문제에서 f(x)는 어느 구간에서 위로 볼록하다- 이런식으로 주지 않거든요.
이걸 수식으로 어떻게 나타내는지 오늘 살펴볼 거에요.

1. 고1 수학 : 내분점과 함숫값의 내분점을 비교. (주로 중점을 사용)
| 아래로 볼록 | 위로 볼록 |
곡선 y=f(x)위의 두 점 A(a, f(a)), B(b, f(b)) (단, a<b)에 대하여 |
곡선 y=f(x)위의 두 점 A(a, f(a)), B(b, f(b)) (단, a<b)에 대하여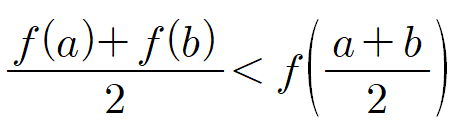 |
 |
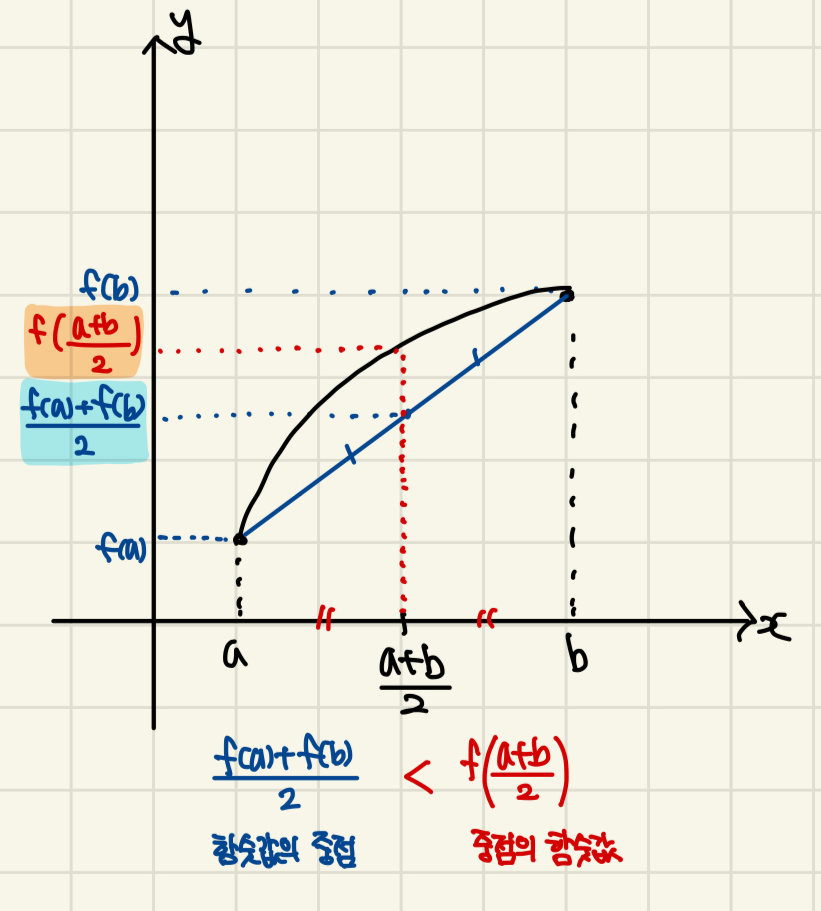 |
만약 아래와 같이 함숫값의 중점과 중점의 함숫값이 항상 같다고 나온다면?

이건 직선을 의미한답니다 :-)
2. 수학2
① 두 평균변화율을 비교하여 판정
| 아래로 볼록 | 위로 볼록 |
| 곡선 y=f(x)위의 두 점 A(a, f(a)), B(b, f(b)), C(c, (c)) (단, a<b<c)에 대하여  |
곡선 y=f(x)위의 두 점 A(a, f(a)), B(b, f(b)) C(c, (c)) (단, a<b<c)에 대하여  |
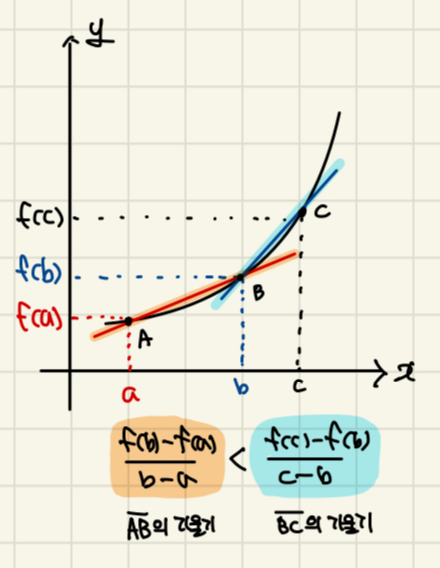 |
 |
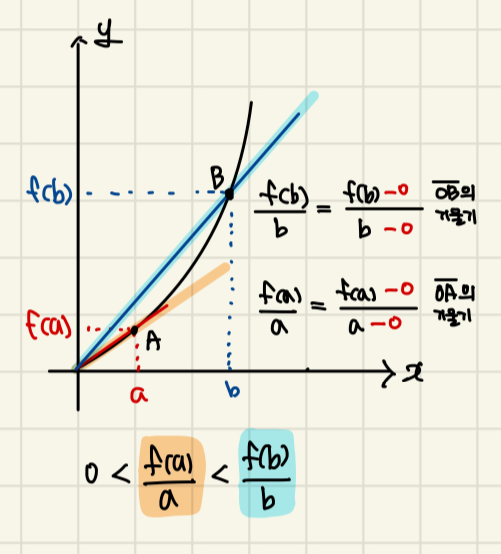
② 원점과 곡선 위의 점을 지나는 직선의 기울기를 이용한 방법
| 아래로 볼록 | 위로 볼록 |
| 원점을 지나는 다항함수 y=f(x)위의 두 점 A(a, f(a)), B(b, f(b)) (단,0< a<b)에 대하여 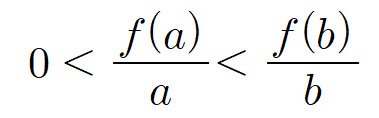 |
원점을 지나는 다항함수 y=f(x)위의 두 점 A(a, f(a)), B(b, f(b)) (단,0< a<b)에 대하여  |
| 0<bf(a)<af(b) | bf(a)>af(b)>0 |
 |
 |
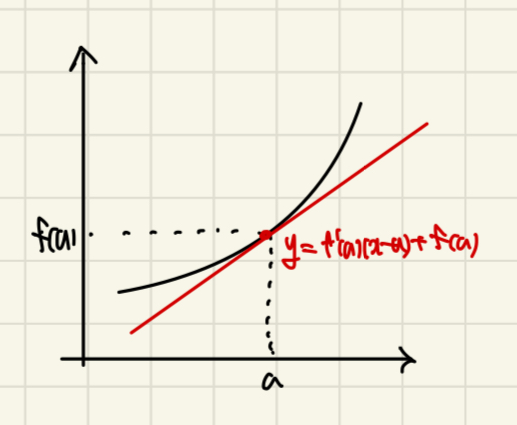
③ 접선의 방정식과 함수의 그래프를 이용한 방법
| 아래로 볼록 | 위로 볼록 |
| x=a에서의 접선이 곡선 y=f(x)의 아래쪽에 있다. | x=a에서의 접선이 곡선 y=f(x)의 위쪽에 있다. |
| f(x) ≥ f'(a)(x-a)+f(a) | f(x) ≤ f'(a)(x-a)+f(a) |
 |
 |
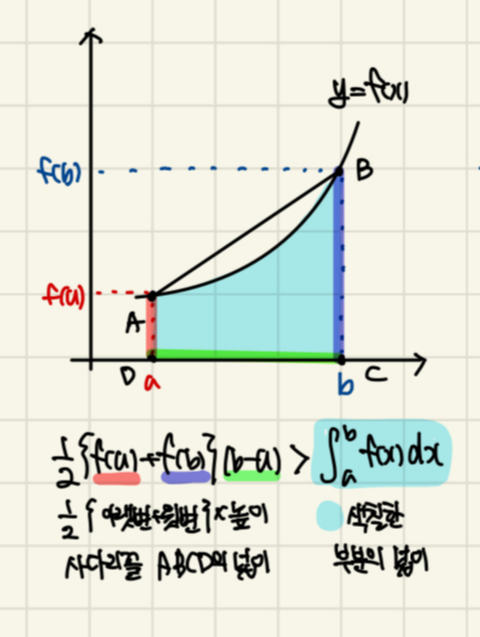
④ 정적분과 사다리꼴의 넓이를 비교하여 판정하는 방법
| 아래로 볼록 | 위로 볼록 |
| 곡선 f(x)≥0 위의 두 점 A(a, f(a)), B(b, f(b)) (단, a<b)에 대하여 | 곡선 f(x)≥0 위의 두 점 A(a, f(a)), B(b, f(b)) (단, a<b)에 대하여 |
 |
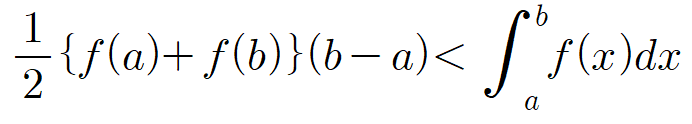 |
 |
 |
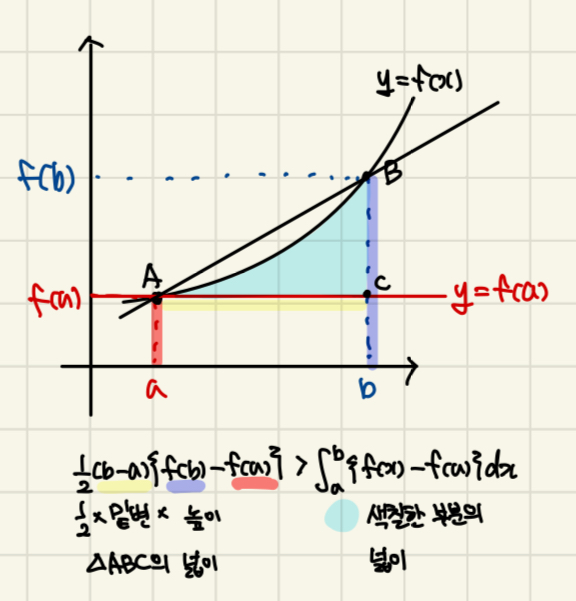
⑤ 정적분과 삼각형의 넓이를 비교하여 판정하는 방법
| 아래로 볼록 | 위로 볼록 |
| 곡선 f(x)≥0 위의 두 점 A(a, f(a)), B(b, f(b)) (단, a<b)에 대하여 | 곡선 f(x)≥0 위의 두 점 A(a, f(a)), B(b, f(b)) (단, a<b)에 대하여 |
 |
 |
 |
 |
미적분까지 배우시면 이계도함수의 부호를 이용하는 방법도 추가 된답니다.
고1때까지만 하더라도 중점을 이용한 방법만 주로 다루는데, 수학2를 배우고나면 함수의 개형을 나타내는 방법이 매우 다양해집니다. 연습을 다양히 해보도록 하세요!
반응형