중학교 1학년때 배운 약수의 개수 문제가
고등학교에서도 그대로 나옵니다.
다만, 총합이나 총곱 등
조금 더 다루는 내용이 많아지죠.
여러개 찾아볼 필요 없이,
오늘은 이 내용을 총정리 해드리겠습니다!

일단 약수는 양의 정수(자연수)만
대상으로 셀 겁니다.
사실 범위를 정해놓지 않으면
무한개라 셀 수가 없습니다.
음, 간단하게 살펴볼까요?

그래서 이를 만족하는 자연수들을 대상으로
약수와 배수를 판정합니다.

그런데 만약 m,n이 자연수가 아니라면?
음수나 분수라면?

사실 더 나아가서 유리수, 무리수도
모두 약수로 가능합니다.
그나마 음의 '정수'까지는 셀 수 있더라도,
이를 넘어가면 개수를 셀 수 없죠.
뭐.. 이 부분은 대학교 과정이므로
더 이상 다루지는 않고 넘어갈게요.
본격적으로 약수를 세러 가봅시다!
일단 약수 문제는
소인수분해를 해둔 상태로 접근합니다.
왜냐하면 어떤 수로 나누어 떨어지는지
알아 보기 쉬운 형태로 둬야 보기 편하니까요.
예시를 같이 살펴보면서 배워볼게요!
108이라는 숫자의 약수를 살펴봅시다.
108을 소인수분해하면
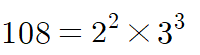
소인수는 2와 3뿐이므로,
다른 숫자는 약수로 가질 수 없습니다.
그리고 소인수인 2와 3도 각각
2개/3개까지만 사용할 수 있죠.
이를 이용하여 표로 나타내보면,
108의 모든 약수를 알 수 있습니다.
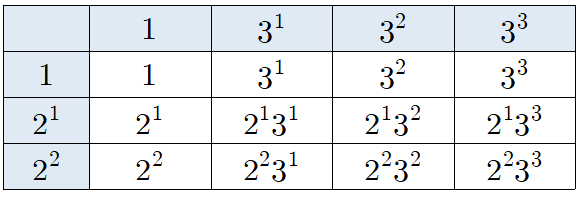
약수의 개수
108의 약수는 총 12개네요.
그런데 이게 어떻게 나왔는지
표를 잘 살펴봅시다.
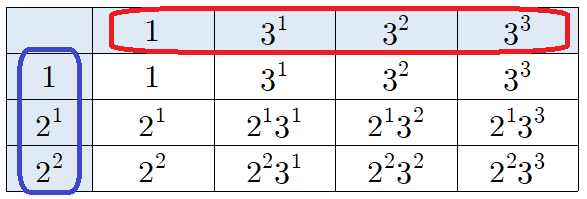
소인수 2는 최대 2개까지 쓸 수 있고, 안 쓸 수도 있죠. 총 3가지 경우가 있습니다.
마찬가지로 소인수 3도 최대 3개까지는 쓸 수 있고, 안 쓸 수도 있습니다. 총 4가지 경우가 있죠.
가로축과 세로축을 살펴보시면 됩니다.
약수란 이 둘의 곱이므로 총 12개가 나옵니다.
(소인수 2의 개수 + 1)(소인수 3의 개수 + 1)
=(2+1)(3+1)=12개가 되는거죠.
+1은 안쓰는 경우까지 센 것입니다.
하나 더 살펴볼까요?
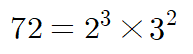
소인수분해한 다음, 소인수의 개수를 살펴봅니다.
해당 소인수를 안 쓰는 경우까지 센다면,
가로와 세로축의 개수가 하나씩 더 늘겠죠?
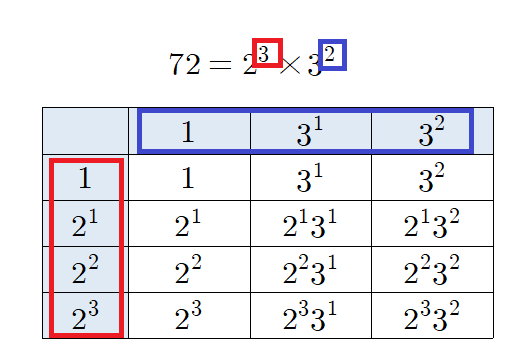
그래서 72의 약수 역시
(3+1)(2+1)=12개가 나옵니다.
약수의 개수에 따른 성질
1. 약수의 개수가 홀수 : 제곱수
홀수x홀수 = 홀수이므로,
모든 소인수가 짝수개 있단 말입니다.
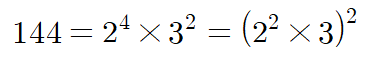
즉 제곱수란 이야기죠.
2. 약수의 개수가 2개 : 소수
이건 소수의 정의니 다들 아시죠?ㅎㅎ
3. 약수의 개수가 3개 : 소수의 제곱수
이 경우는 약수가 1, p, p의 제곱
이렇게 딱 3개만 존재합니다.
약수의 총합
약수를 다 더해봅시다.
역시나 표를 이용하여 살펴볼거에요.
다만, 전체를 한 번에 더하는 건 좀 어려우니,
우선 가로줄을 다 더한다음,
그걸 더해줍시다!
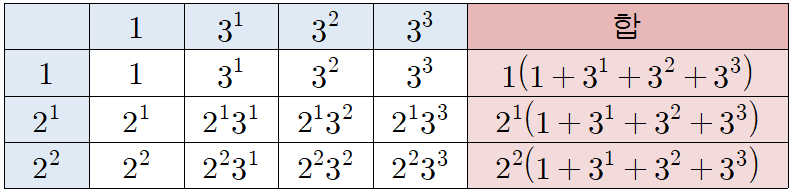
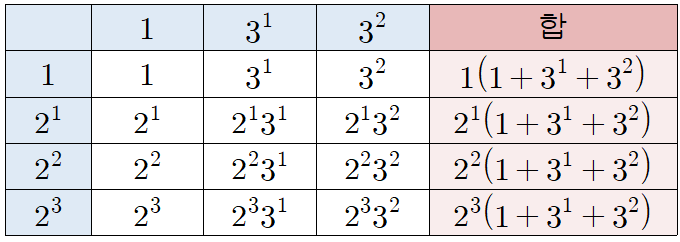
붉은색의 합에서 공통인수가 보이시나요?
공통인수로 묶어서 다 더해주면,
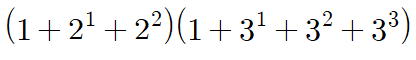
마찬가지로 72도 살펴볼까요?
역시나 붉은색의 합 부분에서 공통인수가 나오므로 같이 정리해서 더해줍니다.
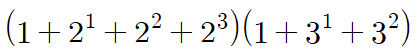
약수의 총곱
이것 역시 표로 보면 쉽습니다.
왜냐하면 약수끼리 곱해서 해당 숫자를 만들 수 있거든요.
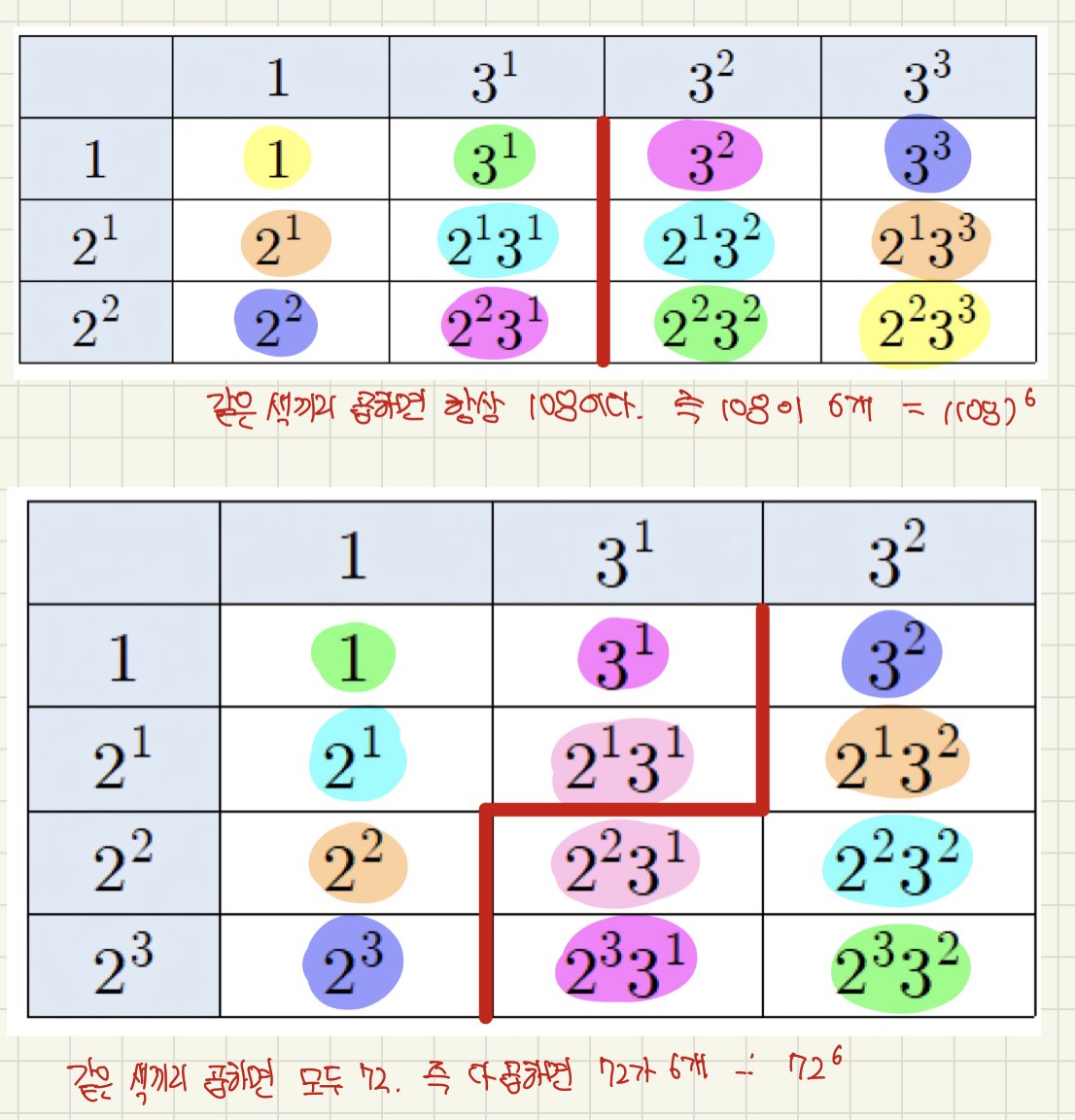
보다시피, 약수끼리는 곱해서 원래의 숫자가 나오는 순서쌍이 있습니다.
그래서 약수의 개수가 짝수개인 경우에는
딱 절반만큼 해당 숫자가 나오는 거죠.
72는 약수의 개수가 12개니까,
약수 다 곱하면 72가 6개 곱해진 모양!
그럼 약수의 개가 홀수개면요..?
약수의 개수가 홀수개란건,
그 수가 제곱수라는 거죠.
그래서 중간에 제곱수가 하나 남습니다.
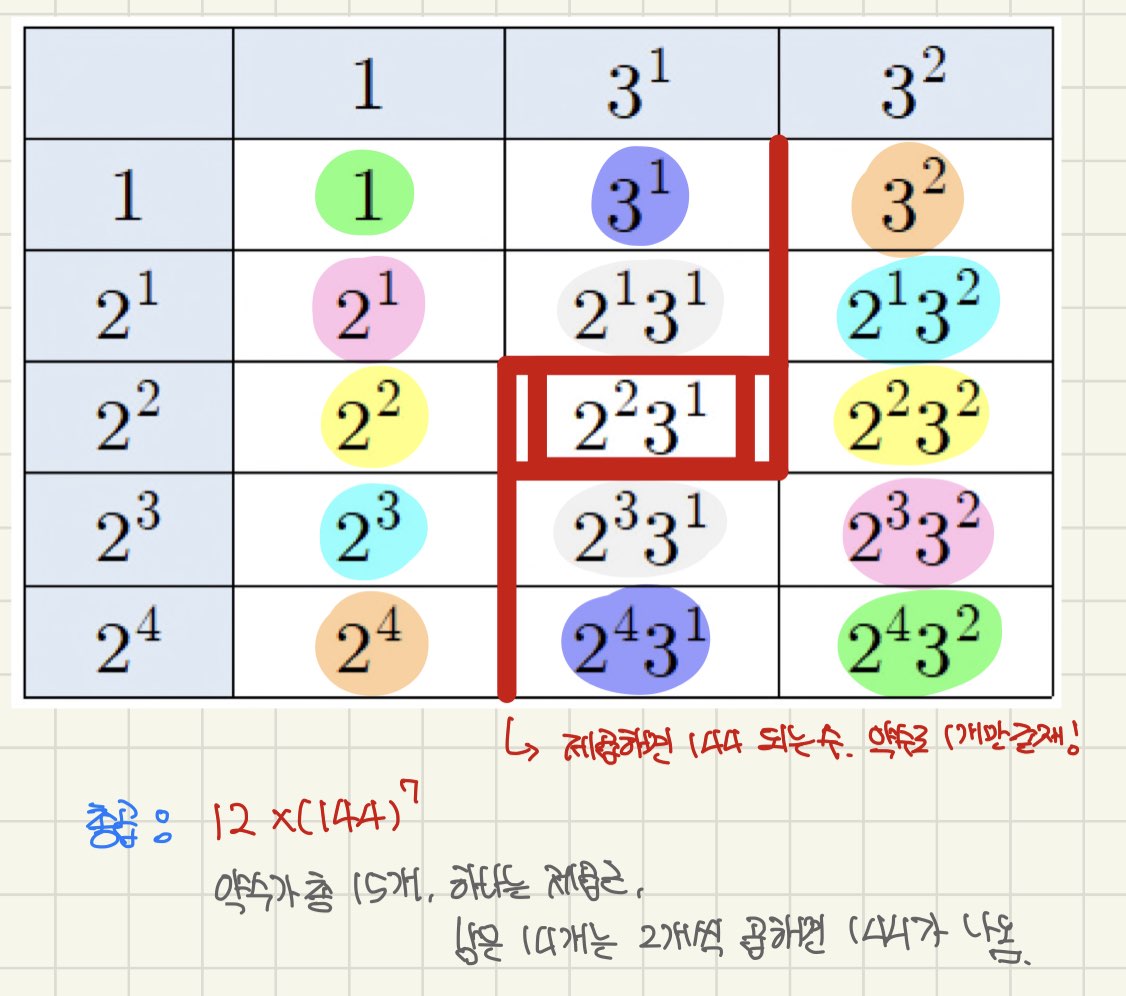
제곱근 하나는 따로 곱해주고,
나머지는 위와 동일하게 계산해주시면 됩니다.
정리 한 번 해볼까요?

일반화 했더니..
문자가 많아서 보기 힘드시죠?
그런 경우, 아래 예시로만 기억하셔도 충분합니다.
단, 표를 그려서 찾았던 방법은
꼭 기억하셔야 해요.^^
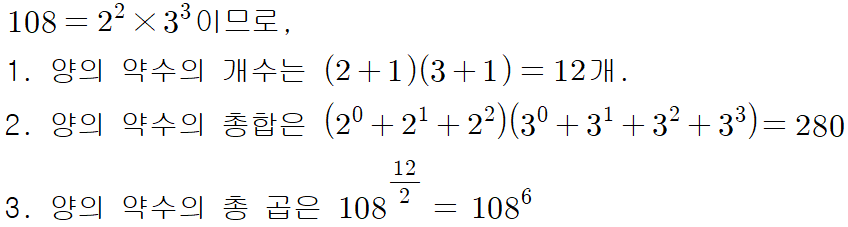
총정리 시리즈 다음에도 이어서 쭉 하겠습니다.^^
그럼 안녕히 계세요!
'고등수학 (2015 개정 교육과정) > 고등수학(하)' 카테고리의 다른 글
| [경우의 수] 시험 꿀팁 교란순열 (완전순열) (0) | 2020.12.05 |
|---|---|
| [경우의 수] 동전문제 지불금액, 지불방법의 수 (2) | 2020.12.04 |
| 산술기하 평균(부등식) - 기하적인 방법으로 증명하기 (0) | 2020.11.24 |
| [귀류법] 루트2가 무리수임을 증명. 무조건 이해되는 설명. (0) | 2020.11.14 |
| 조합과 경우의 수를 이용한 집합의 개수 (0) | 2020.10.18 |