절대부등식의 대표적인 예로
산술기하평균을 이용한 부등식을 배웁니다.
이때, 두 식의 차를 이용하여
증명하는 것이 가장 일반적이지만,
기하적인 방법으로도 증명할 수 있습니다.
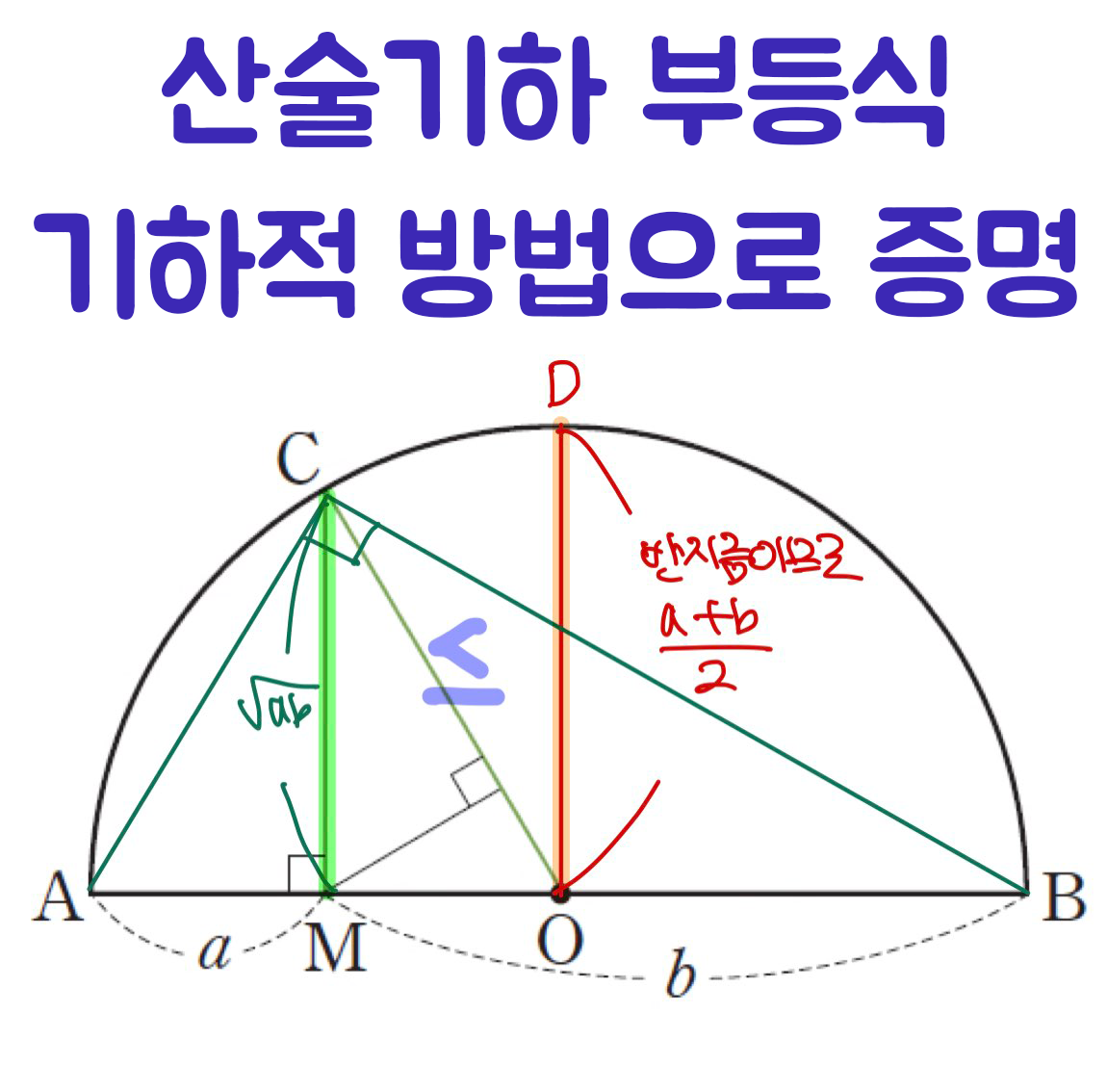
산술기하 부등식의 조건이
변수가 모두 양수일 때이므로,
도형에서 변의 길이로 생각하면,
직관적으로 이해가 됩니다.
산술기하 부등식 증명 첫번째

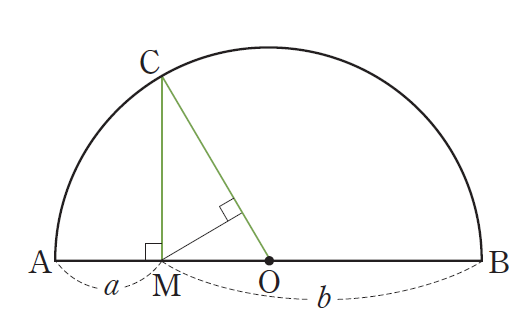
위 그림과 같이 중심이 O이고,
AB를 지름으로 하는 반원을 봅시다.
호 위의 한 점 C를 잡아
수선의 발을 내려줍니다.
양끝으로부터의 길이 중 짧은 것을 a
긴 부분을 b라고 두겠습니다.
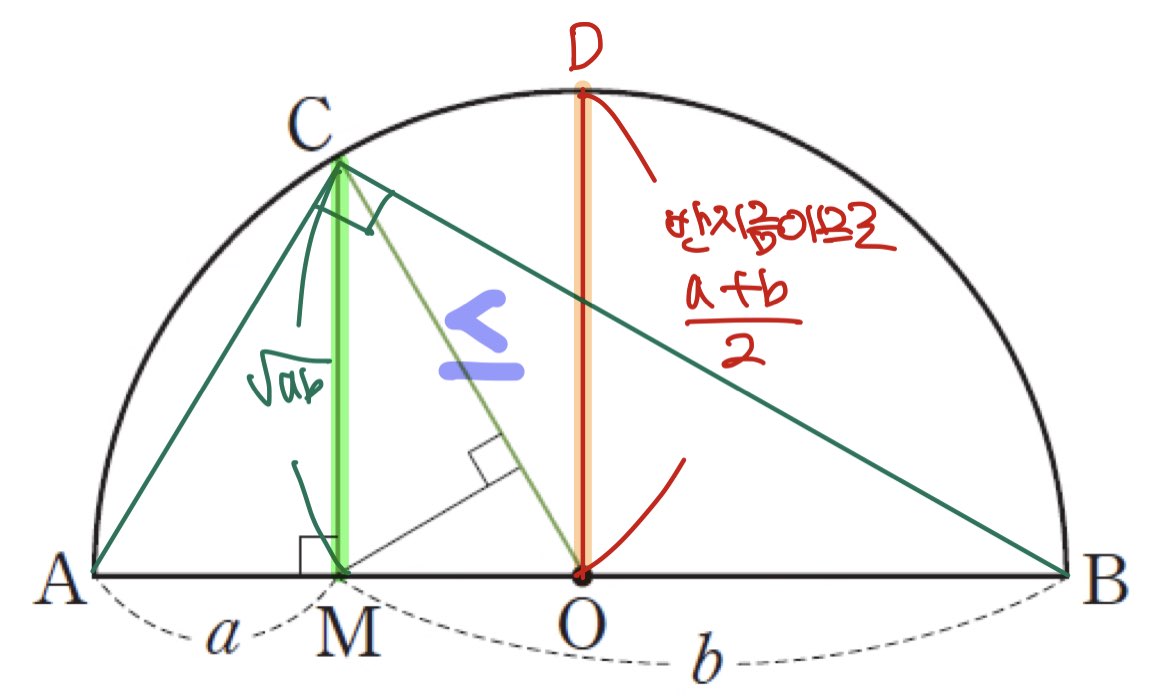
그림에서 보면 아시겠지만,
당연히 DO가 CM보다 깁니다.
언제 같을까요?
a=b일때 성립하겠죠.
DO는 원의 반지름이므로 산술평균이고,
CM은 직각삼각형의 높이이므로
기하평균이 나옵니다.
(혹시 이 부분이 바로 나오지 않는다면,
아래 직각삼각형 포스팅을 참고해주세요.
3번째 닮음을 사용하는 부분입니다.)
https://ladyang86.tistory.com/64
직각삼각형 공식 총정리 (소공식, 피타, 닮음)
중학교 2학년때부터 거의 암기해야 하는 공식이 있습니다. 고3 때까지 지속적으로 계속 나오기 때문에 까먹었다면 계속 복습하셔야 해요. 그래서 사실상 고등학생을 위한 중학교 도형 리마인드
ladyang86.tistory.com
아래는 위의 기하적인 증명을 이용한,
교육청 기출문제입니다.
한 번 가볍게 풀어보세요 :-)

정답은 (가) DC (나)EO입니다.
산술기하 부등식 증명 두번째
이번엔 사각형의 넓이를 이용한
보다 직관적인 방법입니다.
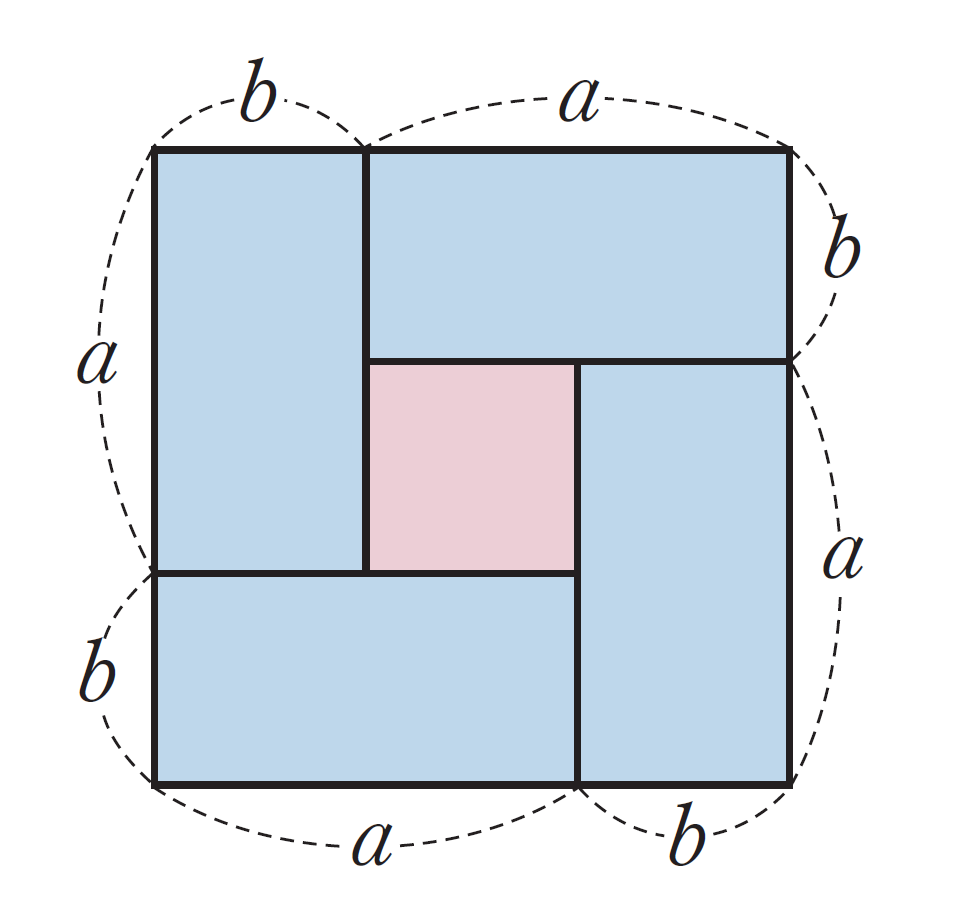
도형의 기하적 성질을 이용하면
절대부등식의 증명을 쉽게 할 수 있습니다.
a,b는 둘 다 직사각형의 변의 길이이므로,
자연스럽게 a>0, b>0인 조건이 설정됩니다.
ⓐ 전체 큰 정사각형의 넓이는
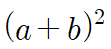
ⓑ 안쪽의 붉은색 작은 정사각형의 넓이는
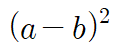
ⓒ 바깥쪽 파란 직사각형 4개의 넓이는
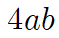
ⓐ=ⓑ+ⓒ입니다.

이 때,
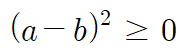
가 성립하므로
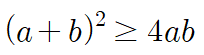
임을 알 수 있습니다.
그리고 a>0, b>0이므로 양변에 루트를 씌워도 부등식은 성립합니다.
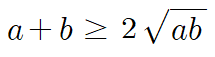
즉 이런 형태가 되죠. 양변을 2로 나눠서 정리하면 됩니다.
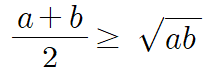
산술평균, 기하평균 외에도
조화평균이 있습니다.
학습량 경감을 이유로
교육과정에서 빠졌죠.
(더불어서 수1의 조화수열도 같이 빠집니다.)
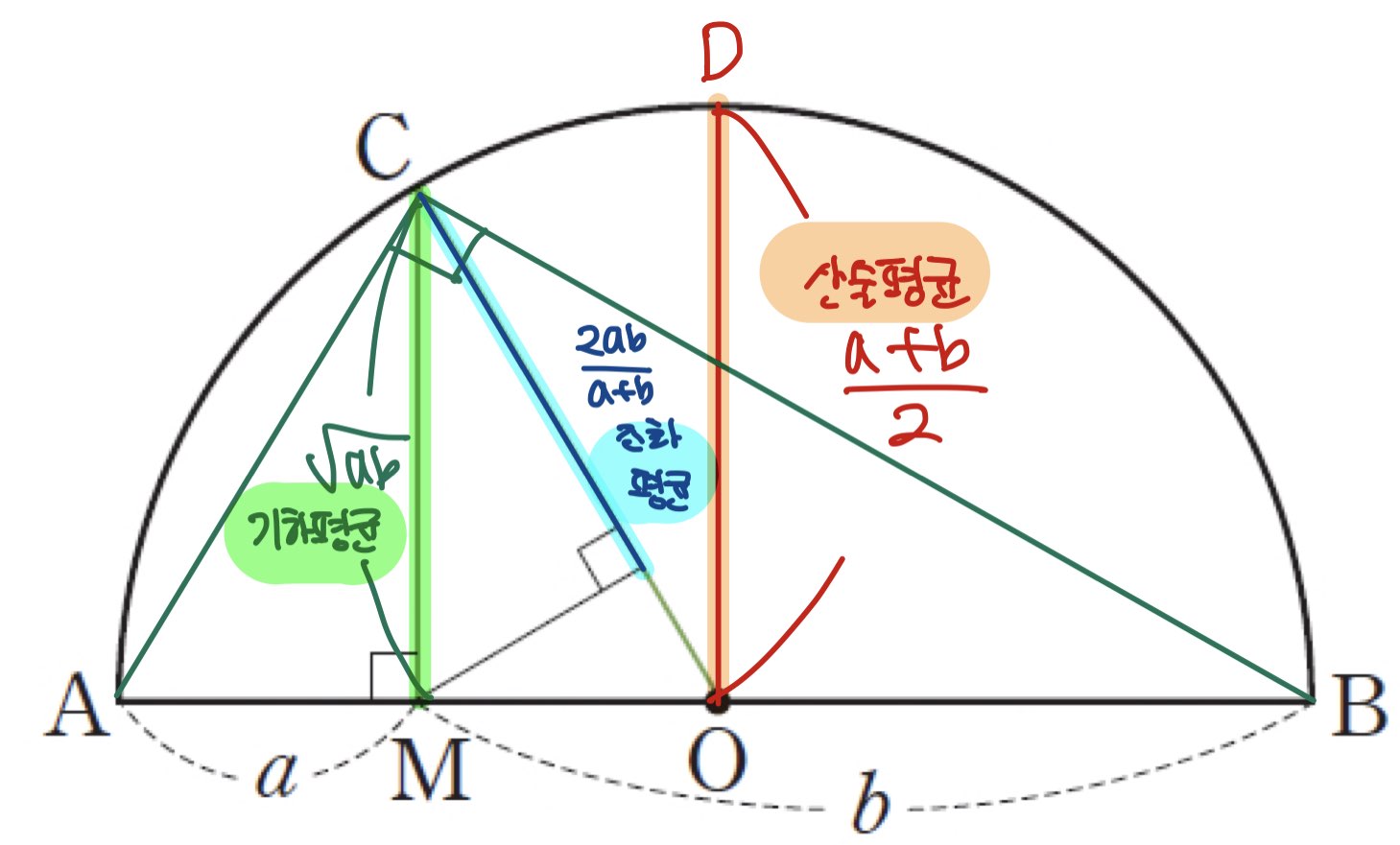
하늘색 부분이 조화평균입니다.
역수가 산술평균을 이루는 수..인데,
교육과정에서 빠졌으니 그냥
저런게 있구나-정도로만 알아도 됩니다.
아니면, 산술평균 부등식을 배운 다음
이걸 위와 같이 기하적으로 증명하고,
심화주제로 조화평균을 같이 다루면
보고서 쓰기에 매우 좋을 거 같긴 하네요.
수학 보고서 주제,
혹은 수학 발표 주제로 추천합니다.
ㅎㅎ
그럼 저는 오늘도 여러분을 응원하며
이만 포스팅을 마치겠습니다.
'고등수학 (2015 개정 교육과정) > 고등수학(하)' 카테고리의 다른 글
| [경우의 수] 동전문제 지불금액, 지불방법의 수 (2) | 2020.12.04 |
|---|---|
| [경우의 수] 양의 약수의 개수와 총합, 곱까지 총정리 (0) | 2020.11.27 |
| [귀류법] 루트2가 무리수임을 증명. 무조건 이해되는 설명. (0) | 2020.11.14 |
| 조합과 경우의 수를 이용한 집합의 개수 (0) | 2020.10.18 |
| [절대부등식] 산술기하보다 쉬운 코시-슈바르츠 부등식 (2) | 2020.10.15 |