오늘은 코시 슈바르츠 부등식을 이용해서, 산술/기하보다 더 편하게 문제를 풀어볼게요!
저번에 했던 포스팅 내용 중, 분자와 분모에 같은 문자가 있는 경우를 다룰 때 입니다.
만약 코시/슈바르츠 부등식이 무엇인지 기억나지 않다면 아래 이전 포스팅을 참고해주세요. ^^
https://ladyang86.tistory.com/50
[절대부등식] 코시 슈바르츠 부등식 증명 및 사용법
오늘은 절대 부등식 중 코시/슈바르츠 부등식에 대해서 알아볼 예정입니다. 우선 코시-슈바르츠 부등식은 아래와 같아요. 증명은 일반적인 부등식 증명법과 같습니다. 그냥 전개해서 빼면 됩니�
ladyang86.tistory.com

산술/기하 부등식을 사용할 때는, 조건이 붙죠?
a>0, b>0 일 때만 사용할 수 있습니다.
a>0일 때는, 아래와 같이 나타낼 수 있죠.

그렇다면, 원래 제곱식으로 되어있는 코시/슈바르츠 부등식을 이렇게 나타내어 줍시다.
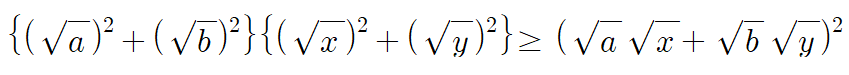
이 식에서 a,b,x,y>0이므로 식을 좀 더 간단하게 써보면,

자 이제 이 형태를 통째로 외우고, 문제에 적용해봅시다.
분모/분자에 같은 문자가 있는 경우,
곱하면 상수가 되므로 간단하게 정리됩니다.
문제1

주어진 식과 구해야 하는 식의 분모/분자에 각각 a,b 라는 문자가 있네요.
그렇다면 같은 문자끼리 곱해질 수 있도록 위치를 바꿔서 코시 슈바르츠 부등식에 대입해주면 됩니다.
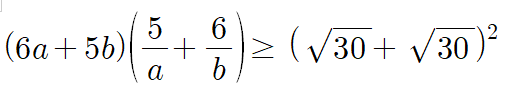
6a+5b=1이라고 이미 문제에서 줬으니, 우리는 우변의 값만 계산하면 되겠네요.
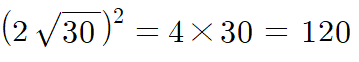
문제2

이것도 분모/분자에 같은 문자가 오는군요..!
앞/뒤에 같은 문자끼리 배치하여, 계산합시다.


참, 쉽죠잉?
이건 문제지에서 꽤나 어려운 문제에 속하는 데, 코시를 이용하여 풀면 아주 간단하게 풀 수 있습니다.
문제3

+2를 +1+1로 쪼개어서 각각 위치시켜줍니다.

최솟값은 4로 바로 나오는군요.!
문제4


문제5

정답 : 최댓값 2√6, a=3/2, b=9/2
문제6

정답 : m=5, a=1/3, b=1이므로 구하는 값은 15
문제7
그림과 같이 ∠ABC= ∠BCD=90º이고,
AB+BC+CD=28일 때,
AD의 거리의 최솟값을 구하시오.



등호는 x+z=y일 때, AB+CD=BC일때 성립합니다.
정답 : 14√2
#1,2,3,5은 산술/기하 부등식으로도 모두 풀 수 있습니다. 다만 코시보다 조금 더 식이 길어지죠.
a>0, b>0이라는 조건은 산술기하 말고도 코시 슈바르츠 부등식에서 일반적인 숫자에도 적용할 수 있다는 것과,
코시 슈바르츠 부등식의 등호 조건을 같이 복습하는 것도 잊지 마시구요.!
그럼 다음에도 유용한 포스팅으로 돌아올게요.^^
'고등수학 (2015 개정 교육과정) > 고등수학(하)' 카테고리의 다른 글
| 산술기하 평균(부등식) - 기하적인 방법으로 증명하기 (0) | 2020.11.24 |
|---|---|
| [귀류법] 루트2가 무리수임을 증명. 무조건 이해되는 설명. (0) | 2020.11.14 |
| 조합과 경우의 수를 이용한 집합의 개수 (0) | 2020.10.18 |
| [절대부등식] 코시 슈바르츠 부등식 증명 및 사용법 (0) | 2020.10.12 |
| [함수] 절댓값이 포함된 함수의 그래프 그리는 방법 (2) | 2020.03.08 |