오늘은 시험 때 시간을 매우 단축시켜주는
꿀팁을 배워 볼 예정입니다.
교란순열(완전순열)이란?
교란순열 : Derangement
완전순열 : Complete permutation
혹은 서브 팩토리얼로 불립니다.
Derangement 에서 D를 따와서,
n개짜리 교란순열을 Dn이라고 씁니다.
정의
n개의 원소가 모두
자기 자신이 아닌 값으로 배정되는 순열
(모든 원소의 위치를 바꾸는 순열)
말이 좀 어렵죠?
아래 예제를 통해서 이해해봅시다.
아마 꼭 한 번씩은 보셨을 거에요:-)
예제1
학생을 An이라 하고
각자의 시험지를 an이라 합시다.
시험지를 바꿔서 채점한다고 할 때,
자신의 시험지는 자신이 채점하지 않을 때,
채점하는 방법의 수가 Dn입니다.
예제2
X={1,2,3,...,n}
f : X->X로의 일대일함수 일때,
f(x)≠x인 함수의 개수도 Dn입니다.
교란(완전)순열의 개수
점화식이나 일반항 등이 존재하긴 하지만,
기본적으로 고등수학 수준에서는
“수형도”로 직접 세는 걸 목표로 합니다.
D1=0입니다.
한 명 뿐일 땐, 자기 시험지 외의 것을 채점할 수 없으니까요.
D2=1입니다.
서로 바꾸는 방법 1가지만 존재합니다.
D3는 수형도를 그려서 세볼까요?
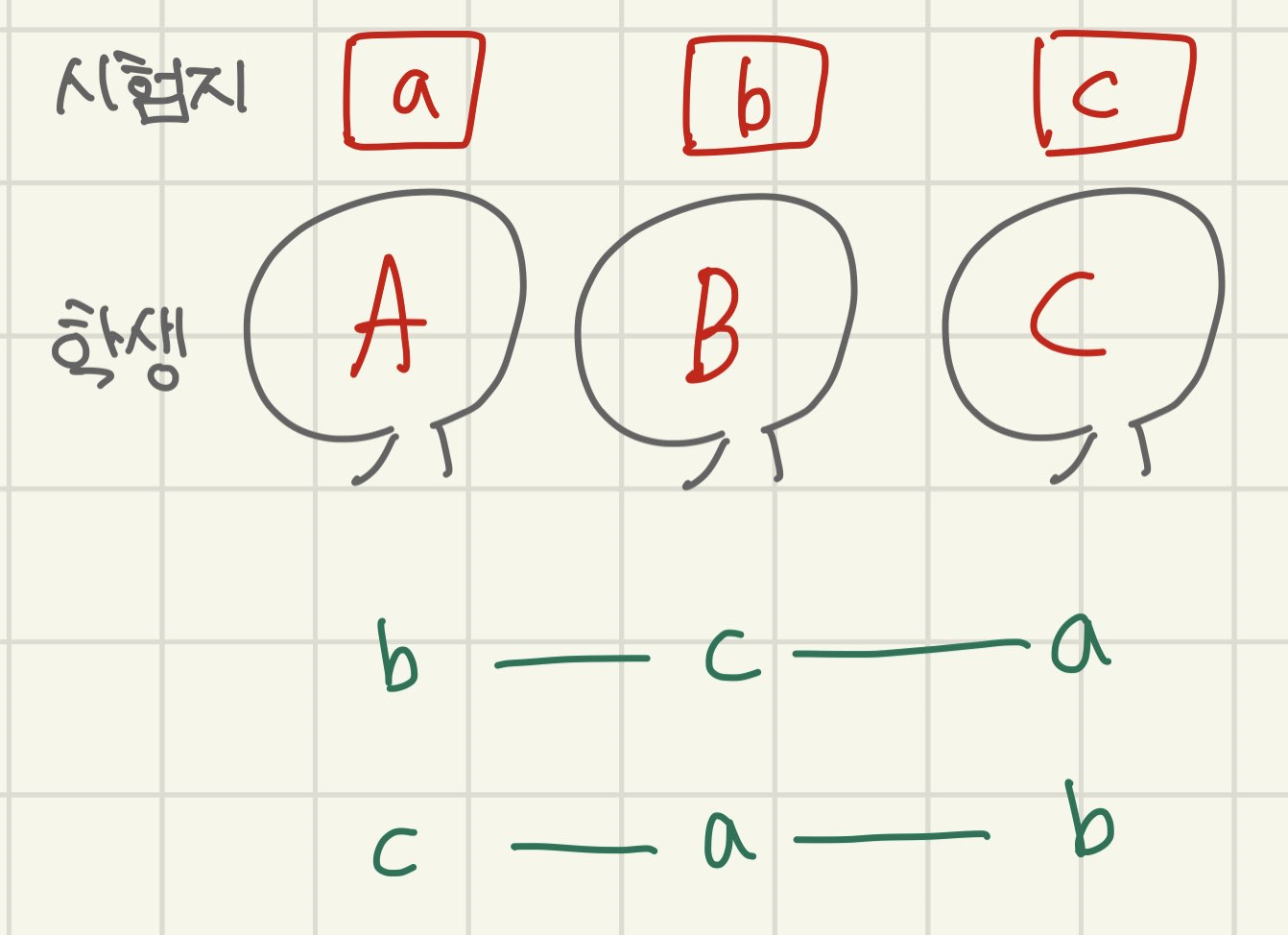
뭔가 많이 나올 것 같았지만,
자기 자신의 것을 선택하지 않는다는
조건 때문에 의외로 적게 나옵니다.
그럼 시험에서 가장 잘 나오는
D4를 한 번 세어볼까요?
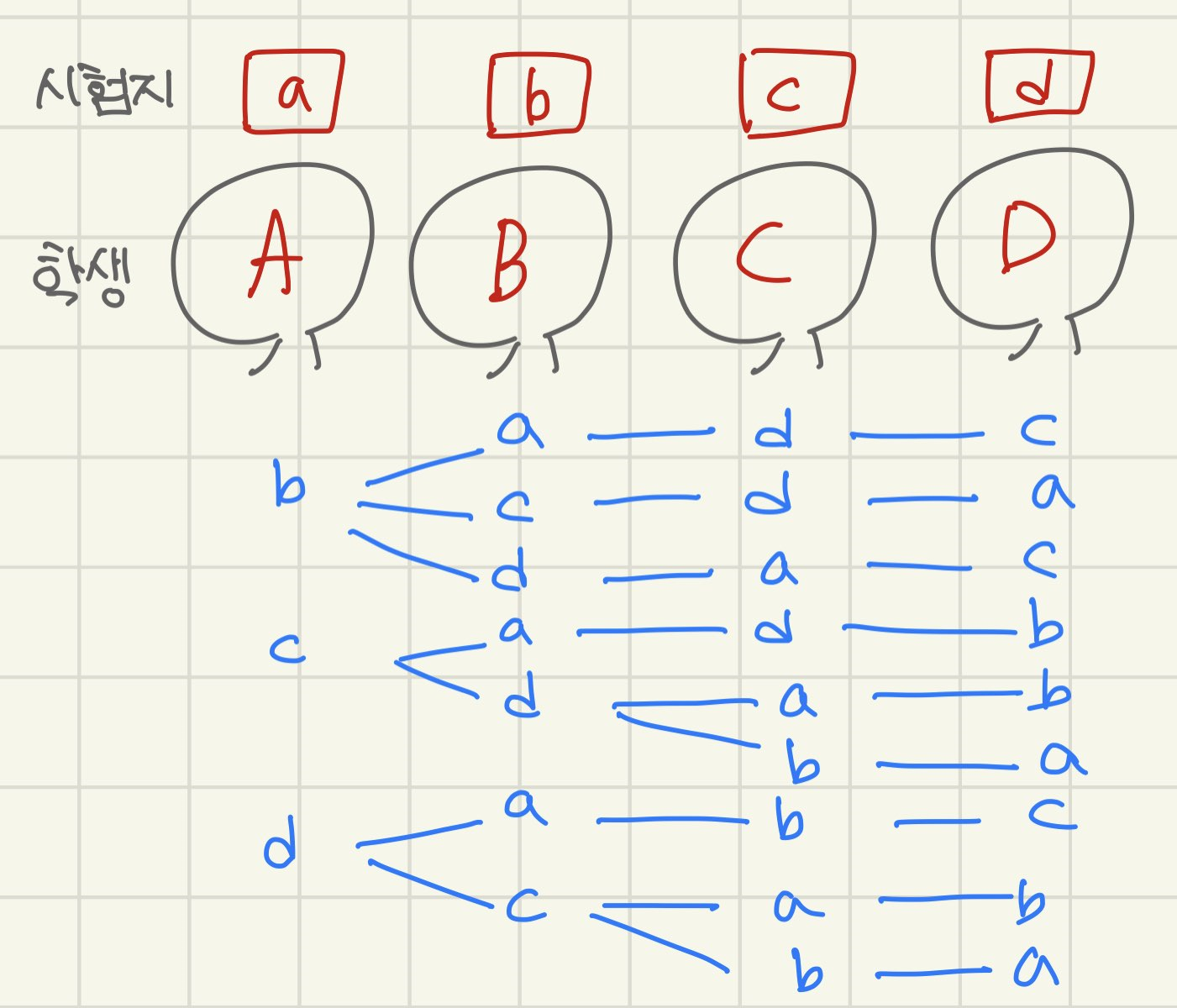
개수도 9개 정도로 적당한 편이라,
시험에서 상당히 자주 나옵니다.
서술형으로 나온다면 직접
위의 수형도를 다 그리셔야 합니다.
그런데 문제 풀 때 그냥 D4=9 정도는
외워주시는 게 좋습니다.
하나씩 수형도 그리는 시간도 아깝잖아요?
D5는 개수가 많아서
실제로 그리라고 나오진 않으니,
그냥 44개라고 외워줍시다.
사실 수형도는 n이 5보다 커지면
실제로 그려서 세기가 많이 힘들기에..
거의 안 나온다고 보시면 됩니다.
(점화식이 교육과정에서 빠진 이상,
더더욱 그러하죠.)
그래서 자주 나오는 D4는
개수를 외워버리는 것이 편합니다.
직접적으로 D4를 묻는 문제도 나오지만,
조합과 섞어서 나올 수 있으니,
한 번 풀어볼까요?
응용문제
한량의 친구들 7명이서 송년파티를 한다고 모였다.
거하게 술을 마시고, 각자 헤어졌다.
각자 신발을 신고 집에 갔는데,
다들 술 취해서 그런지, 손님 7명 중
자기 신발을 제대로 신고 들어간 사람은 3명이었다.
경우의 수는 얼마인가?
7명 중 3명은 자기 신발을 제대로 신었으니,
제대로 신은 사람을 정해줍시다.
그게 7C3=35가지네요.
나머지 4명은 모두 다른 사람의 신발을 신었으니,
D4=9입니다.
따라서 구하는 경우의 수는,
35 x 9 = 315개입니다.
이렇게 문제 풀 때 알려고,
하나씩 수형도 다 그리면 너무 오래 걸리니
오늘 이 포스팅을 본 김에 외워둡시다^^

내용이 길어져서 교란순열의 점화식과 일반항에 대해서는 다음에 이어서 포스팅 할게요! 고등 수학만으로도 이해하는데 크게 어려운 내용은 아니어서 관심가시는 분들은 같이 보시면 좋을 듯 합니다.
그럼 다음에 만나요^^
'고등수학 (2015 개정 교육과정) > 고등수학(하)' 카테고리의 다른 글
| 서로 다른 주사위 경우의 수 문제 총정리 (합,차, 그 외 기타) (0) | 2020.12.13 |
|---|---|
| 유리함수 절댓값 그래프 그리기 (0) | 2020.12.10 |
| [경우의 수] 동전문제 지불금액, 지불방법의 수 (2) | 2020.12.04 |
| [경우의 수] 양의 약수의 개수와 총합, 곱까지 총정리 (0) | 2020.11.27 |
| 산술기하 평균(부등식) - 기하적인 방법으로 증명하기 (0) | 2020.11.24 |