오늘은 선분의 내분점/외분점 문제 중 가장 많이들 헷갈려하는 선분의 길이비를 다룰까 합니다.

내분, 외분에 대한 정확한 정의와 개념이 없으면 풀기가 힘든 유형이죠. 공식보다는 선분을 m:n으로 내분/외분 한다는 의미를 먼저 복습하셔야 합니다.
1. 주어진 식을 비례식으로 표현합니다.
이 때 필요한 선행지식은
a:b=c:d이면 bc=ad라는
기본적인 것이죠 :-)
2. 좌표를 알고 있는 점을 찍고
등분점으로 나타냅니다.
3. 남은 점을 좌/우로 나누어
해당 길이비에 맞게 찍어준다.
4. 내/외분점으로 해석하여,
공식을 적용한다.
문제1
A(5,-2), B(-1,4)를 지나는 직선 AB위에 있고,
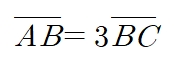
를 만족시키는 점 C의 좌표를 모두 구하시오.
해설
1. 주어진 식을 비례식으로 표현합니다.
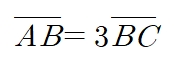
를 비례식으로 나타낸다면,

2. 좌표를 알고 있는 점을 기준으로
등분점으로 나타냅니다.
여기서는 A와 B의 좌표를 알고 있으니
A,B를 표기해보도록 할게요.
비례식에서 AB의 길이비가 3이므로
수직선에 세 칸(등분점)을
표기하여 줍니다.

3. 다시 식을 살펴볼까요?

AB의 길이가 3칸일 때,
BC의 길이는 1칸이죠.
그러니, B로부터 한칸에 해당하는 길이만큼
왼쪽/오른쪽으로 가서 점을 나타내면 됩니다.

4. 내/외분점으로 해석하여,
공식을 적용합니다.

문제2
A(-3,-2), B(1,4)를 지나는 직선 AB위의 점
C(a,b)에 대하여 3AB=2BC일 때,
b-a의 값을 구하여라. (단, a>0)
해설
1. 주어진 식을 비례식으로 표현합니다.

를 비례식으로 나타낸다면,

2. 좌표를 알고 있는 점을 기준으로
등분점으로 나타냅니다.
여기서는 A와 B의 좌표를 알고 있으니
AB의 길이비가 2이라고 보고
수직선에 등분점과 함께 나타냅니다.

3. 남은 하나의 점을
왼쪽/오른쪽으로 나누어
해당 길이비에 맞게 찍어줍니다.

그러니까 B로부터 세칸에 해당하는 길이만큼
왼쪽/오른쪽으로 가서 점을 나타내면 됩니다.

4. 내/외분점으로 해석하여,
공식을 적용합니다.

문제3
두 점 A(-4,3), B(2,6)을 잇는
직선 AB위의 점 C(a,b)에 대하여
삼각형 OAC의 넓이가
삼각형 OBC의 넓이의 2배일 때,
a+b의 값은?
(단, O는 원점이고 a>0이다.)
이것 역시 그림으로 그려서 해석하면,
점 C가 AB의 2:1 외분점입니다.
그럼 화이팅!
'고등수학 (2015 개정 교육과정) > 고등수학(상)' 카테고리의 다른 글
| 항등식 중 조립제법으로 푸는 유형 정리 (조립제법의 중복 사용) (0) | 2022.02.26 |
|---|---|
| 96%의 학생이 틀리는 방정식, 부등식 문제 (0) | 2022.01.09 |
| 원 위의 점에서의 접선 빨리 구하는 팁! (2) | 2021.09.02 |
| [원 접선의 방정식] 극선의 방정식 (0) | 2021.06.26 |
| 삼차방정식 f(ax+b)=0의 근에 관한 문제 (합,곱 쉽게 풀기) (0) | 2021.06.11 |