이건 기본문제 말고 내신에 나올만한 삼각함수 도형 고난도 선별 문제입니다. 풀이를 다 올리자니 시간이 너무 오래 걸릴 것 같아 일단 문제와 정답 업로드부터 합니다. 풀이는 차차 올릴 예정이에요. :-) 뭐.. 내신 기간 전에는 업로드 하겠죠..?;
문제 1
아래 그림과 같이 AB=2, AC=5이고, ∠CAB=60º인 삼각형 ABC가 있다. ∠CAB의 이등분선이 원과 만나는 점을 D, 선분 AC가 원과 만나는 점을 E라 할 때, 두 선분 CD, CE와 호 DE로 둘러싸인 부분과 선분 BD와 호 BD로 둘러싸인 부분의 넓이의 합을 구하시오.

정답 : 95√3 / 98
문제 2
아래 그림과 같이 AB=7, AC=9, sin(∠BAC)=(4√3)/7 인 삼각형 ABC의 꼭짓점 A에서 선분 BC에 내린 수선의 발을 H라 하자. 선분 AH를 지름으로 하는 원이 선분 AC와 만나는 점 중 A가 아닌 점을 P라 할 때, 선분 CP의 길이는? (단, ∠BAC는 예각)

정답 : 36/7
문제 3
그림과 같이 중심이 O이고 반지름의 길이가 3√3인 원에 내접하는 예각삼각형 ABC에 대하여 △OAB:△OAC=1:2√2이고, BC=3√6일 때, △OAC의 둘레 길이는?

정답 2번 6√2 + 6√3
문제 4
정삼각형 ABC가 반지름의 길이가 r인 원에 내접하고 있다. 선분 AC와 선분 BD가 만나고 BD=2가 되도록 원 위에 점 D를 잡는다. ∠DBC=θ라 할 때, sinθ=√3 / 3이다. 반지름의 길이 r의 값은?

정답 : 1번
문제 5
DA=3AB, ∠DAB=2π/3이고 반지름의 길이가 2인 원에 내접하는 사각형 ABCD가 있다. 두 대각선 AC, BD의 교점을 E라 할 때, 점 E는 선분 BD를 2:3으로 내분한다. 사각형 ABCD의 넓이가 (q√3)/p일 때, p+q의 값은? (단, p와 q는 서로소인 자연수이다.)

정답 : 48
문제 6
그림과 같이 AB=8, BC=7, CA=5인 삼각형 ABC에 내접하는 원의 중심을 O라 하자. 직선 AO가 선분 BC와 만나는 점을 D라 할 때, 선분 AD의 길이는?

정답 : 3번 (40√3) / 13
문제 7
그림과 같이 반지름의 길이가 3인 원 O에 내접하는 사각형 ABCD에 대하여 AB=BC=√6, AD+CD=8일 때, 사각형 ABCD의 넓이는?

정답 : (16√5)/5
문제 8
AB=AC=6√6 + 6√2 인 이등변삼각형 ABC가 있다. ∠BAC=30º이고, 선분 BC를 지름으로 하는 원이 있다. 이 원에 내접하는 삼각형 DEF의 면적이 54일 때, EF=d, DF=e, DE=f라 하자. d×e×f의 값을 구하시오.

정답 : 1296
문제 9
그림과 같이 원 O에 내접하는 △ABC가 있다. AB=3, AC=4, ∠BAC = π/3이고 △ABC에서 ∠A의 외각의 이등분선이 원 O와 만나는 점을 D, △ABC에서 ∠A의 내각의 이등분선이 원 O와 만나는 점을 E라 할 때, 사각형 AECD의 넓이는?

정답 : 10√3 / 3
문제 10
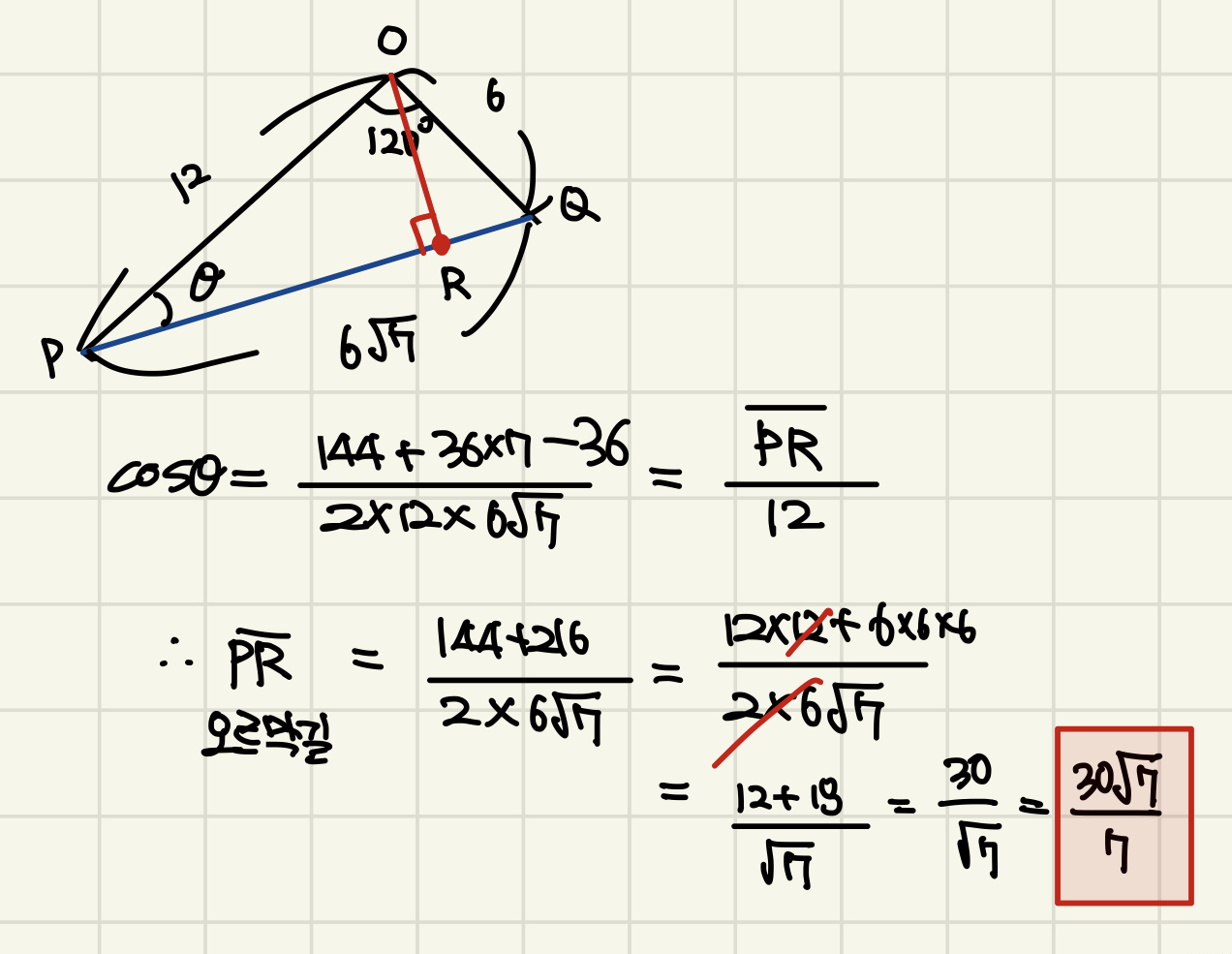
그림과 같이 밑면의 반지름의 길이가 4cm이고, 모선의 길이가 12cm인 원뿔이 있다. 원뿔의 밑면인 원의 둘레 위의 점 P에서 모선 OP의 중점 Q까지 원뿔의 표면을 따라 최단 거리로 개미 한 마리가 기어갈 때 어느 지점까지는 오르막길이고 이후 내리막길이 된다. 오르막길의 거리를 구하시오.




문제 11
그림과 같이 AB=7, BC=8, CA=5인 삼각형 ABC에서 꼭짓점 A를 중심으로 하고 반지름의 길이가 3인 원과 꼭짓점 B를 중심으로 하고 반지름의 길이가 5인 원이 삼각형 ABC의 내부에서 만나는 점을 P라 하자. 점 P에서 변 AB, BC, CA에 내린 수선의 발을 각각 D, E, F라 할 때, DE+DF의 값은?

정답 : (7√3) /2
문제 12
그림과 같이 길이가 2인 선분 AB를 지름으로 하는 반원의 호 AB 위를 움직이는 점 C가 있다. 점 C에서 선분 AB에 내린 수선의 발을 H, 호AC의 중점을 D라 하고, △ABC의 넓이를 S, △BCH의 넓이를 T라 하자. S:T=9:4일 때, △ACD의 넓이를 구하시오.

정답 : √5/9
문제 13
그림과 같이 삼각형 ABC에서 BC=6, AC=8이고, 선분 AB위의 점 D와 선분 AC위의 점 E에 대하여 AE=BE=BC, ∠BDE=∠BEC를 만족한다. 이때, 선분 DE의 길이를 구하시오.

정답 : (6√21)/7


만약 모의고사 고난도 문제도 풀어보고 싶다면 아래 포스팅 참고하세요.
https://ladyang86.tistory.com/181
삼각함수 활용 도형 고난도 문제 모음 - 모의고사, 수능 기출
역시나 일단 문제부터 풀어보려고 올리는... 기출 베이스의 삼각함수의 활용 도형 고난도 문제입니다. 우선 문제와 정답부터 업로드하고, 풀이는 차차 업데이트 할게요. 문제1 2022학년도 6월 평
ladyang86.tistory.com
'고등수학 (2015 개정 교육과정) > 수학1' 카테고리의 다른 글
| [부분 분수] 분수 꼴로 이루어진 수열의 합 (0) | 2023.02.24 |
|---|---|
| 삼각함수 각변환 총정리 (0) | 2023.02.05 |
| 교과서 점화식 연습용 문제 모음 (표현법까지만+문제만) (0) | 2022.06.29 |
| 지수/로그함수 평행이동, 직선과의 교점 문제 (0) | 2022.06.29 |
| 첫째항부터 수열을 이루기 위한 합 조건 (0) | 2022.06.12 |