지수로그함수와 직선의 교점
지수함수, 로그함수를 평행이동시킨 모양과 직선의 교점을 구하는 문제를 몇 개 다뤄볼까 합니다.

일반적인 방정식으로는 지수함수와 다항함수, 로그함수와 다항함수의 해를 구하기 힘듭니다. 그러니 교점이 주어졌다고 해서 직접 둘을 연립해서 푼다고 생각하지 마세요.!
직선의 경우에는 기울기를 적극 이용하셔야 하고, 지수/로그 함수는 어떻게 평행이동했는지를 잘 살펴보시면 의외로 쉽게 풀 수 있습니다. 예제를 몇 개 풀어보면서 익혀보도록 해요 :-)
문제 1
2022 수능특강 수학1 Ch2. Lv3 #1


우선 두 로그함수의 관계를 살펴봅시다. 밑이 같으므로 평행이동된 모습이죠.
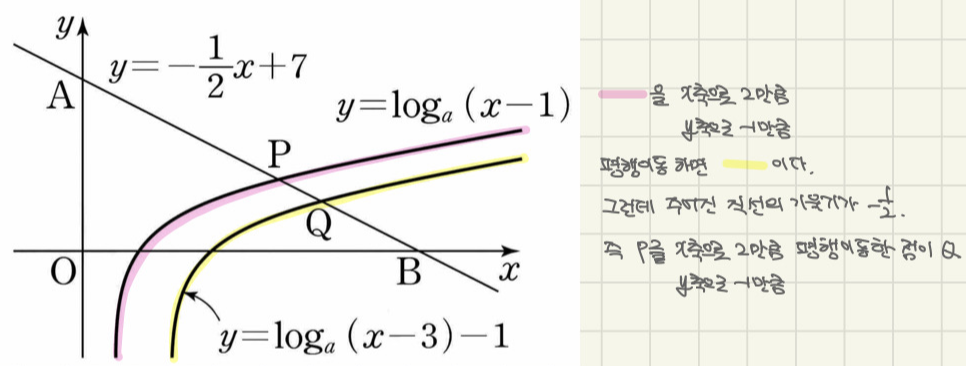
그런데 마침 주어진 직선의 기울기도 -1/2입니다. 즉, P를 평행이동 시켰더니 Q가 된 것이죠!

PQ와 AB의 길이를 구할 수 있고,
나머지도 변의 길이비를 알기 때문에
금방 구할 수 있답니다.

Q의 좌표든 P의 좌표든 편한 것 구해서 대입하시면 됩니다.
길이비를 이용한다면 금방 구할 수 있죠.

2022 대수능 수학#9
직선 y=2x+k가 두 함수

의 그래프와 만나는 점을 각각 P,Q라 하자. PQ=√5일 때, 상수 k의 값은?

주어진 직선의 기울기가 2인데, 두 점 사이의 거리가 √5이므로, P와 Q 사이의 위치관계를 파악할 수 있습니다.

P를 평행이동한 것이 Q이죠. 그래서 P의 좌표를 설정하고, 이에 맞게 Q의 좌표를 정한 다음, 각각의 함수에 넣고 연립해주시면 됩니다.

k=17/3이 나오네요 :-)
위 함수 모양을 좀 더 살펴볼게요.
노란함수의 그래프를 평행이동하면 핑크색 함수가 되죠!
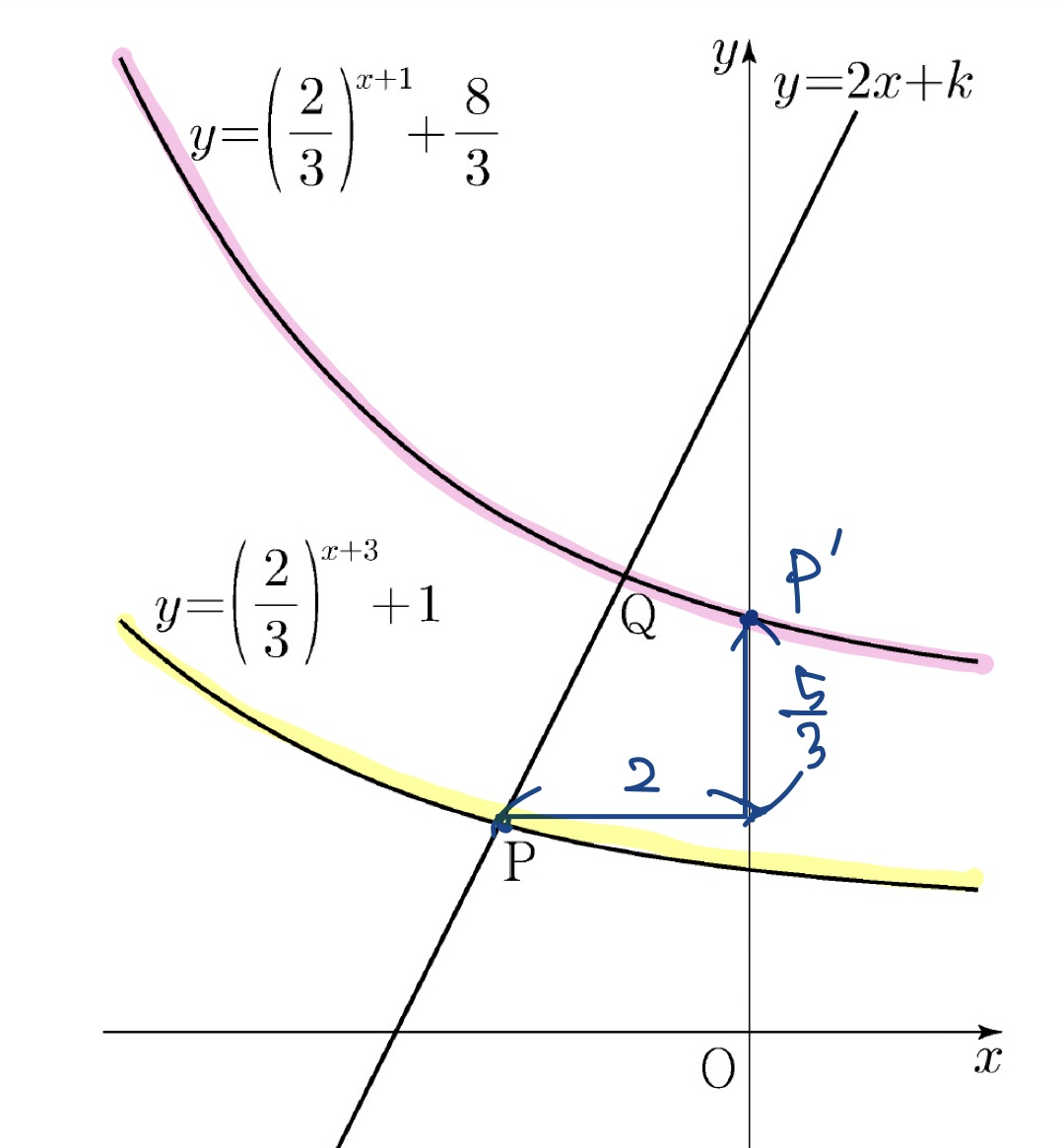
그런데 평행이동하는 길이가 x축으로 2만큼, y축으로 5/3만큼 이동하는 것이므로 이동한 점의 좌표는 Q와는 다른 점이 됩니다. 마침 식에서 구한 값으로는 P의 x좌표가 -2였으니 P를 이동킨 점은 핑크색 함수의 y절편이 되겠군요 :-)
문제 3
2023 수능특강 수학1 Ch2. Lv2 #7


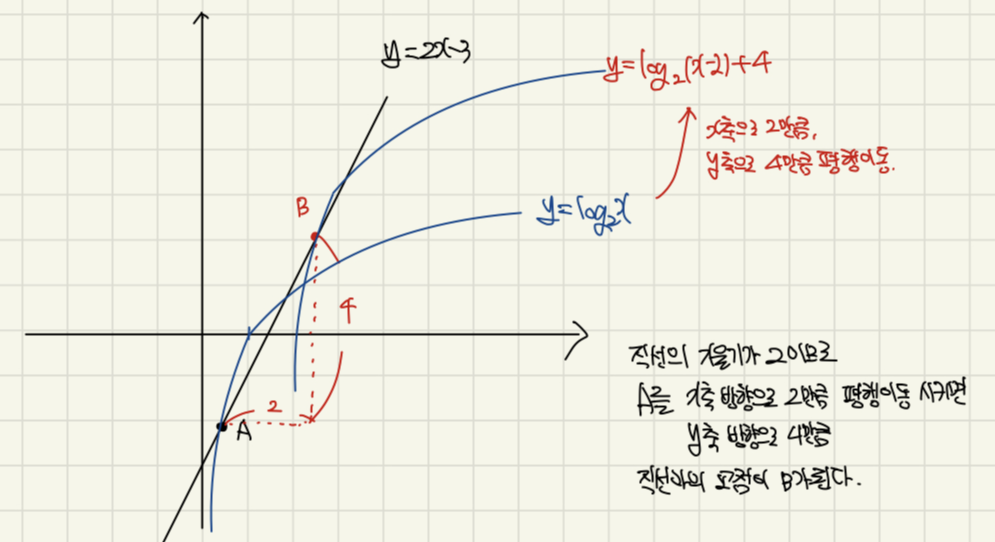

위의 두 문제의 차이점을 발견 하셨나요? 평행 이동한 변화량이 함수의 기울기와 같은 경우에는 교점위로 그대로 이동이 됩니다. 아닌 경우에는 길이와 같은 정보가 주어진다면 얼만큼 이동했는지 정확하게 알 수 있죠.
꼼꼼하게 잘 풀어보고 내용 잘 익히도록 해요 :-)
아래는 추가된 문제입니다.
위와 같은 논리로 풀면 굉장히 쉽게 풀린답니다.
2023 수능완성 모의고사 5회 #13


2025 수능특강 수학1 Ch2. Lv2 #4

정답 : 29
'고등수학 (2015 개정 교육과정) > 수학1' 카테고리의 다른 글
| 삼각함수 활용 도형 고난도 문제 모음 - 내신용 (0) | 2022.08.12 |
|---|---|
| 교과서 점화식 연습용 문제 모음 (표현법까지만+문제만) (0) | 2022.06.29 |
| 첫째항부터 수열을 이루기 위한 합 조건 (0) | 2022.06.12 |
| [부분합] 등차수열의 합도 등차수열, 등비수열의 합도 등비수열 (0) | 2022.06.04 |
| 탄젠트 점근선의 방정식 완전 정복 (0) | 2022.05.26 |