부분합으로 이루어진 수열
오늘은 등차수열과 등비수열의 부분합으로 이루어진 수열을 살펴볼까 합니다. 간단하게 결론부터 이야기하자면, 앞에서부터 차례로 같은 개수로 끊어서 더하면 등차수열의 합은 등차수열, 등비수열의 합은 등비수열이에요.

이걸 이용하면 빨리 풀 수 있는 문제가 많기 때문에 한 번 익힌 다음 오래오래 써먹어봅시다.
등차수열의 합은 등차수열
간단합니다. 등차수열을 n개씩 잘라서 더해볼게요.
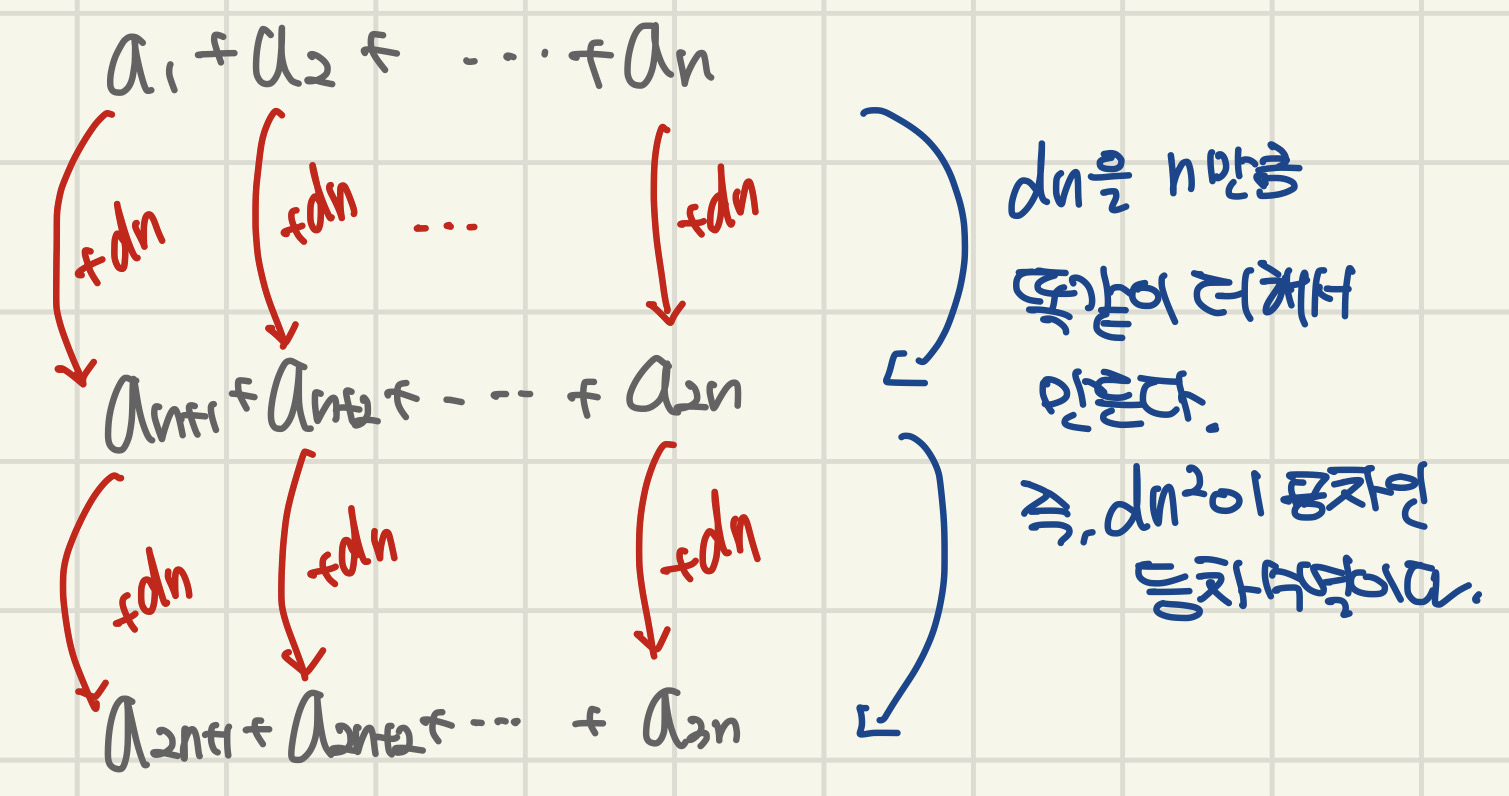
즉, 합끼리의 차도 항상 동일하기 때문에, 이 역시 등차수열입니다.
문자로 쓰니 조금 어려운가요? 좀 더 쉽게 예제를 풀면서 익혀보도록 할게요.
예제 1
등차수열 {an}의 첫째항부터 제 n항까지의 합을 Sn이라 하자. S5=25, S10=75일 때, S15의 값을 구하시오.
앞에서부터 5개씩 잘라서 더한 다음 관찰을 해봅시다.

사실 50이 등차 중항이므로 바로 50x3=150으로 계산해도 됩니다. 그렇지만 일단 5개씩 잘라서 더한 값 역시 등차수열이란 걸 기억해 두면 좀 더 좋겠죠?
다음은 등비수열을 살펴봅시다.
등비수열의 합은 등비수열

역시나 마찬가지입니다. n개씩 잘라서 더한 부분합의 경우 역시나 등비수열임을 알 수 있죠. 등비수열의 경우에는 같은 항의 개수만큼 잘라서 더하면, 공비를 바로 계산하기도 매우 쉬운 편입니다.
개인적으로 특히나 등비수열의 합의 경우, 공식에 거듭제곱이나 분수꼴이 계속 나와서 제가 계산이 좀 하기가 싫어서.. 나름 유용하게 쓰고 있달까요?
아무튼 이것도 예제를 풀어보면서 익혀보도록 합시다.
예제 2
등비수열 {an}의 첫째항부터 제 n항까지의 합을 Sn이라 하자. S10=10, S20=30일 때, S30의 값을 구하시오.
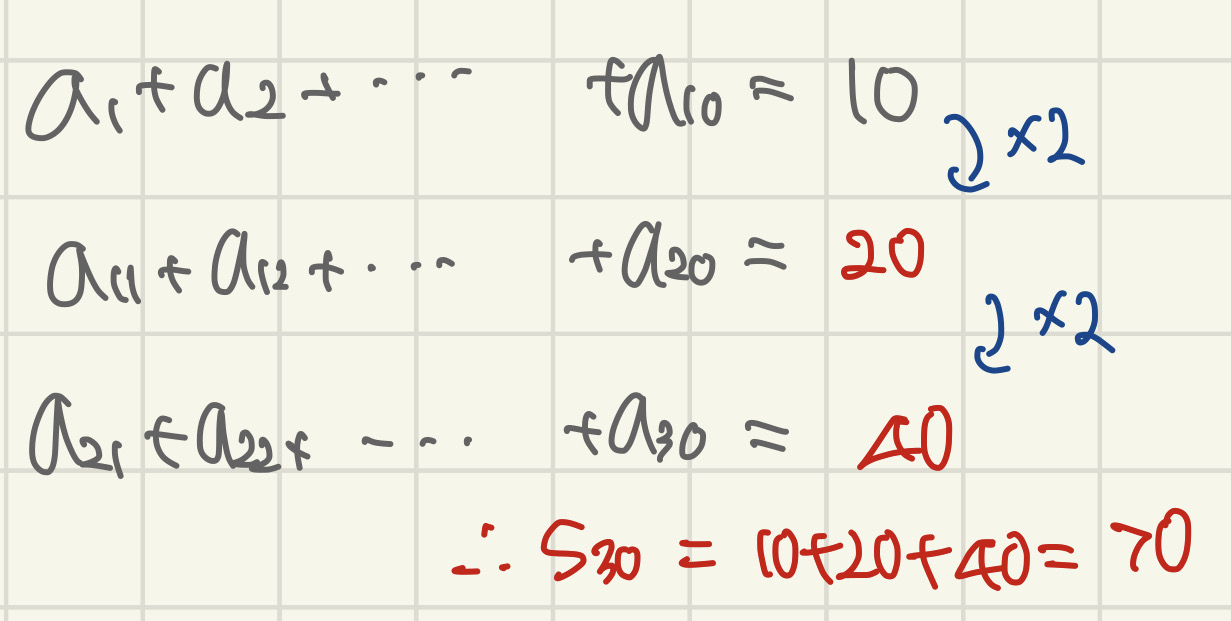
수열은 계산하는 시간이 꽤나 걸리는 편이니 여러가지 팁들을 알고 계시면 시험 볼 때 도움이 꽤 많이 된답니다.
나중에 같은 내용인데 다른 유형이라 다뤄야하는 문제들이 있다면 좀 더 추가로 올려보도록 할게요.
그럼 열공하세요!
'고등수학 (2015 개정 교육과정) > 수학1' 카테고리의 다른 글
| 지수/로그함수 평행이동, 직선과의 교점 문제 (0) | 2022.06.29 |
|---|---|
| 첫째항부터 수열을 이루기 위한 합 조건 (0) | 2022.06.12 |
| 탄젠트 점근선의 방정식 완전 정복 (0) | 2022.05.26 |
| [지수함수, 로그함수] 성질 설명 문제 모음 (0) | 2022.04.26 |
| [지수] 거듭제곱근 실근의 개수 (내신 선별) (0) | 2022.04.17 |