고대 그리스 수학자인 아폴로니우스가 발견한,
아폴로니우스의 원을 다루어 보려고 합니다.
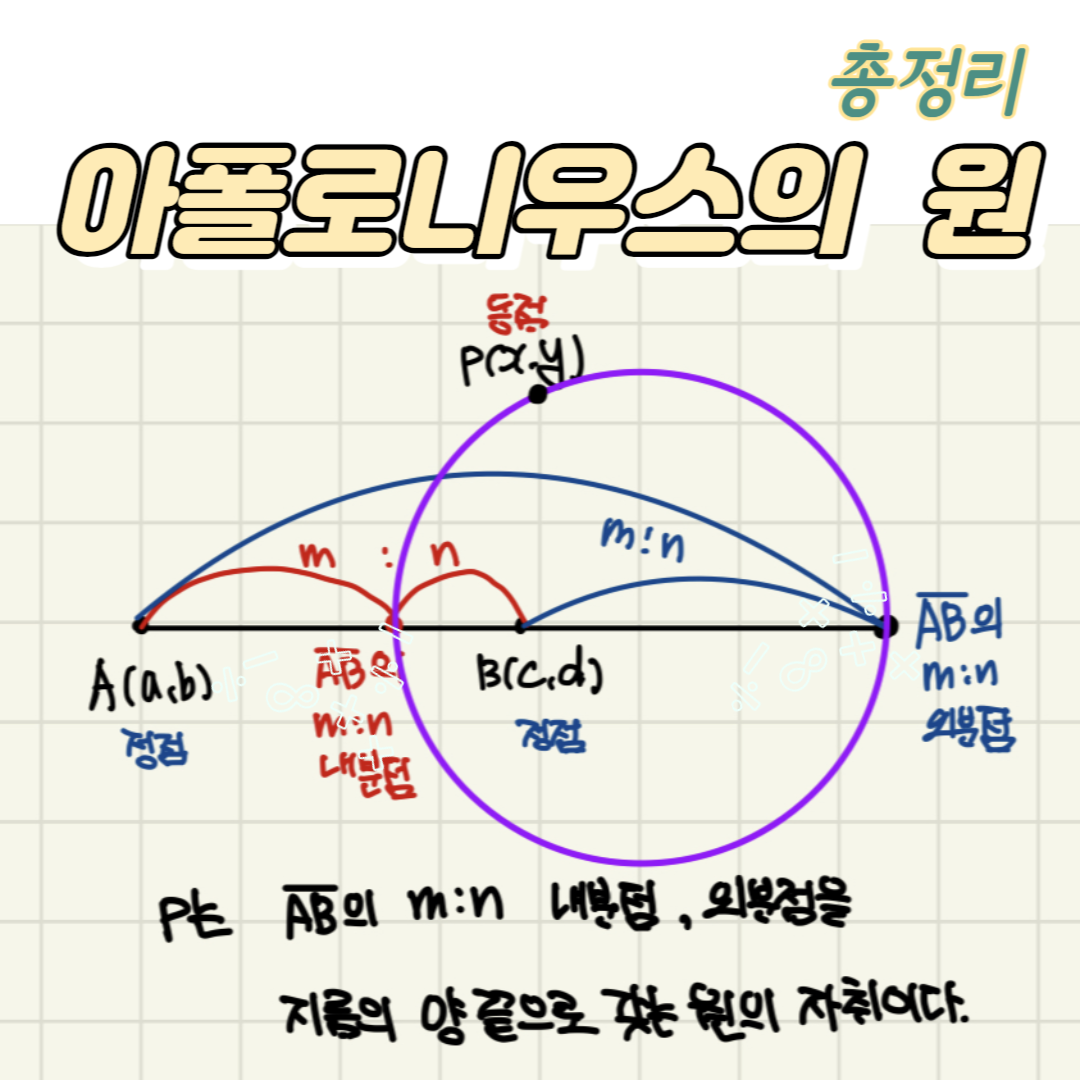
아폴로니우스의 원
정의 : 두 점으로부터 거리의 비가 일정한 점들의 집합
두 정점으로 부터 거리의 비가 m:n이 되는 점 P(x,y)의 자취를 구해봅시다.

여기서 원이 되려면 m과 n은 달라야겠죠?
만약 m=n이라면, 이차항이 모두 소거돼서 직선이 나온답니다. (수직 이등분선)
아폴로니우스의 원의 기하학적 의미
: 두 정점을 m:n으로 내분하는 점과 외분하는 점을 지름의 양 끝으로 하는 원

아폴로니우스의 원 관련 대표 유형 몇 가지를 풀어볼게요.
문제1 (기본유형 - 원의 방정식 구하기)
두 점 A(3, -1), B(-3, 5)로부터의 거리의 비가 1:2인 점의 자취는 원을 나타낸다. 이 원의 반지름의 길이는?

문제2 (최대각의 크기)
두 점 A(-1, 1), B(2, 1)로부터의 거리의 비가 2:1인 점 P에 대하여 ∠PAB의 크기의 최대일 때, 선분 AP의 길이를 구하여라.
y의 좌표가 같으므로 내분점/외분점을 이용하는 편이 훨씬 간단하다.
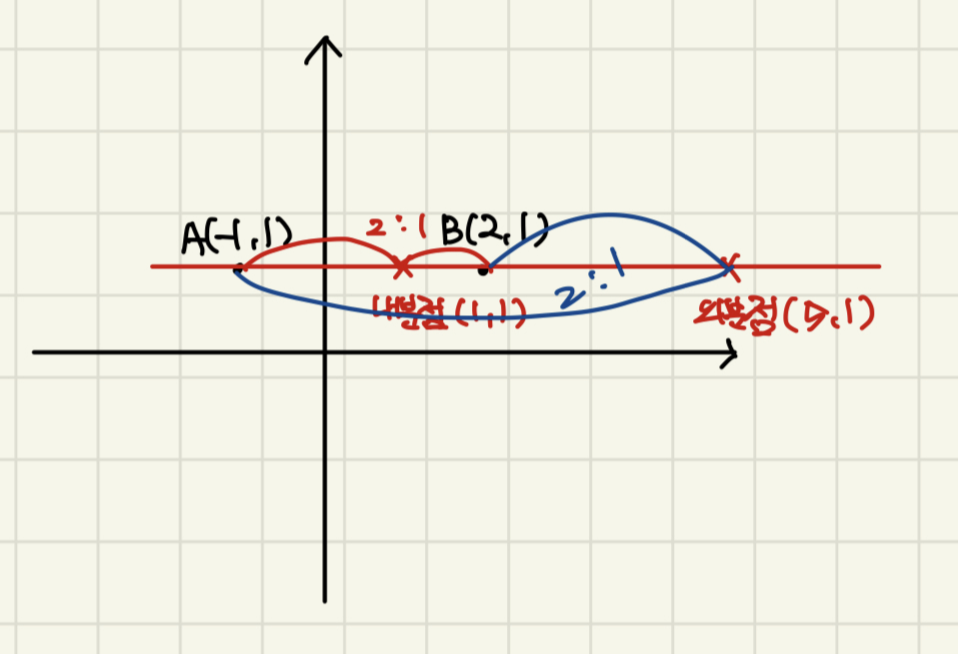

원 위의 점 P 중에서 각PAB가 최대가 되는 점은 아래와 같이 접점일 때이다.

문제3 (실생활 응용)
바다 위에 8km만큼 떨어진 두 지점 A,B에 각각 배가 한 대씩 위치해 있다. 두 배는 두 지점 A,B를 동시에 출발하여 일정한 속력으로 중간에 방향을 바꾸지 않고 직선 경로로 이동하고, 지점 A에서 출발하는 배의 속력이 지점 B에서 출발하는 배의 속력의 3배이다. 두 배가 동시에 도달할 수 있는 지점을 P라 할 때, 삼각형 ABP의 넓이의 최댓값은?
(단, 두 배의 크기는 고려하지 않고, 움직일 수 있는 바다는 충분히 넓다.)
A의 속력이 B의 속력의 3배이므로, 같은 시간 안에 가는 거리는 A가 B보다 3배 더 멀리 갈 수 있다. 즉, AP:BP=3:1이다.
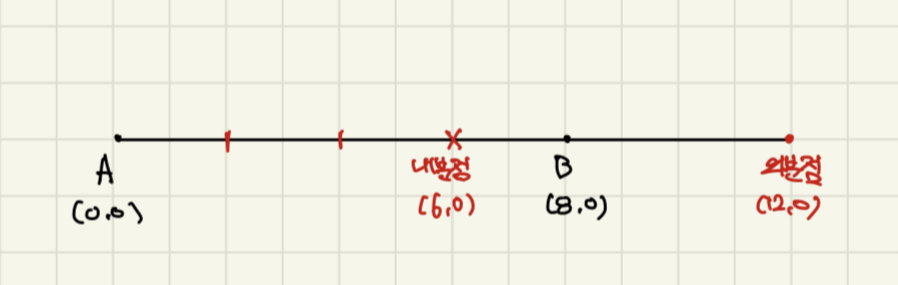

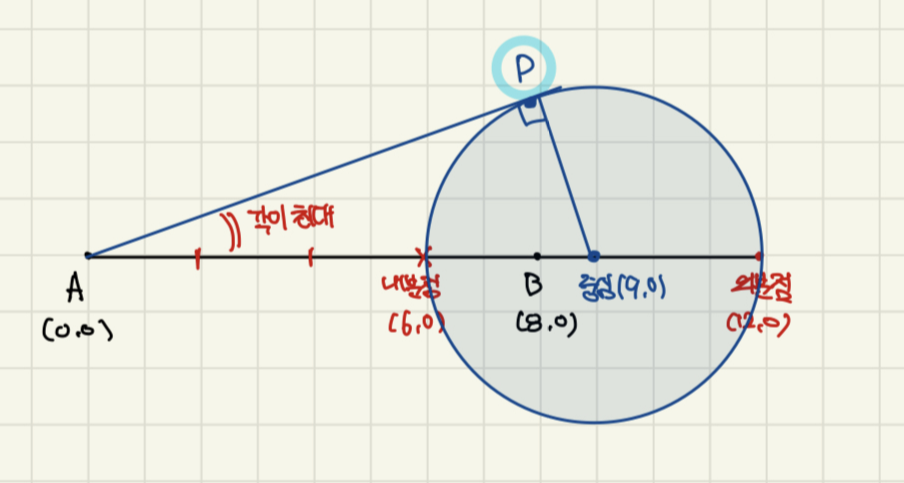
두 점 A,B를 좌표평면으로 갖고 와서 A(0,0), B(8,0)으로 두면, 둘 다 x축 위에 있는 점이므로 선분의 내외분점으로 원을 만드는 편이 더 빠르다.

위에서 풀어본 두 유형은 잘 나오는데, 각이 최대냐, 삼각형의 넓이가 최대냐에 따라 점 P를 잡는 기준이 달라집니다.

(240912추가함)
문제4
좌표평면 위의 세 점 A(-1, -2), B(5, 1), C(a, b)를 꼭짓점으로 하는 삼각형 ABC에서 ∠ACB를 이등분하는 직선과 선분 AB의 교점이 x축 위에 있을 때, 삼각형 ABC 넓이의 최댓값은?

정답 : 15
각의 이등분선을 이용하면 비율이 정해지므로, 이걸 이용하여 문제를 낼 수도 있습니다.
각의 이등분선의 교점이 내심이니, 문제에서 내심이라고 줄 수도 있어요.
그럼 열공하세요~! ^^
'고등수학 (2015 개정 교육과정) > 고등수학(상)' 카테고리의 다른 글
| [도형의 이동] 평행이동 대칭이동 최단거리 고난도 문제 (0) | 2023.09.24 |
|---|---|
| 도형의 이동 - 선대칭 최단거리 푸는 방법 (거리합의 최솟값) (0) | 2023.07.15 |
| 내신용 - 고차식 나머지 문제 선별 (0) | 2023.05.13 |
| 복소수 실수 조건 응용 문제 (0) | 2023.04.07 |
| 복소수 부호 (근호 조건) 총 정리! (0) | 2023.04.02 |