도형의 이동에서 주로 다루는 선대칭 최단거리 기본 문제를 다 푸셨다면 도전해볼만한 고난도 문제를 몇개 실어봅니다. 이론과 기본 문제는 아래 포스팅 참고하시면 됩니다. (사실 기본기만 알아도 정점을 주는 대부분의 문제는 거의 다 풀립니다.)
도형의 이동 - 선대칭 최단거리 푸는 방법 (거리합의 최솟값)
고1 수학에서 배우는 최단거리 구하는 방법에 대해 오늘 알려드리고자 합니다. 기본적으로 필요한 배경지식은 아래와 같습니다. 오늘 배울 상황은 아래와 같습니다. 이 문제를 푸실 때는 반드시
ladyang86.tistory.com
이번에 실은 문제들은 건너야 하는 강이 2개인 문제와 동점으로만 구성된 문제들이에요.
(문제와 풀이는 틈틈이 업데이트 될 수 있습니다.)
문제1
아래 그림과 같이 AB=√5, BC=3, CA=2√2인 삼각형 ABC에 대하여 세 선분 AB, BC, CA 위의 양 끝 점을 제외한 임의의 점을 각각 P, Q, R라 하자. 삼각형 PQR의 둘레의 길이의 최솟값은?

정답 : (6√10)/5
문제2
<그림>과 같이 x축에 평행한 두 직선 l1, l2로 둘러싸인 폭이 4인 강A와 직선 3x-4y=0과 평행한 두 직선 l3, l4로 둘러싸인 폭이 5인 강 B를 사이에 두고 집과 병원이 위치한다. 병원은 집에서 x축 방향으로 27만큼, y축 방향으로 -26만큼 평행이동한 지점에 위치한다. 집에서 출발하여 최단거리로 병원에 갈 수 있도록 강 A와 B에 각각 다리를 설치하려고 한다. 이때, 집에서 출발하여 다리를 통해 강을 건너 병원에 도달하는 최단거리는? (단, 다리를 건널 때 이동거리는 강의 폭과 같으며 강의 폭은 강을 둘러싼 두 직선 사이의 거리이다.)
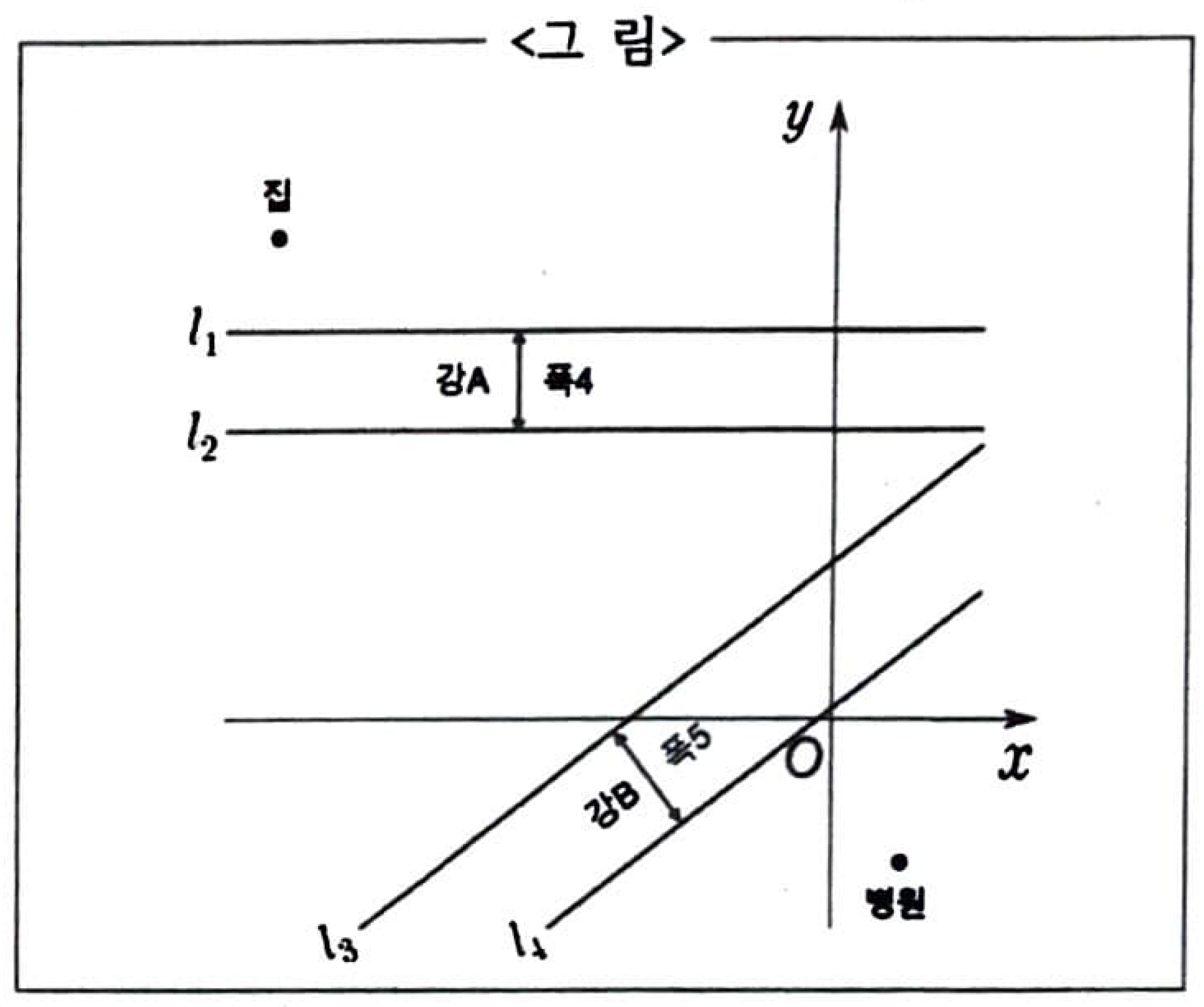
정답 : 39
문제3
그림과 같이 반지름의 길이가 4이고, 중심각의 크기가 60도인 부채꼴 BOA의 호 AB 위에 두 점 A,B가 아닌 점 P를 잡았다. 두 변 OA, OB 위를 움직이는 점을 각각 Q,R라 할 때, 삼각형 PQR의 둘레의 길이의 최솟값은?

정답 : 4√3
'고등수학 (2015 개정 교육과정) > 고등수학(상)' 카테고리의 다른 글
| [내신] 나머지 정리 - 낯선 문제 모음 (1) | 2024.04.20 |
|---|---|
| 판별식의 판별식 (D of D) 꼭 써야 하나요? (일차식의 곱으로 인수분해) (0) | 2024.02.15 |
| 도형의 이동 - 선대칭 최단거리 푸는 방법 (거리합의 최솟값) (0) | 2023.07.15 |
| 아폴로니우스의 원 - 두 점으로부터 거리의 비가 같은 점의 자취 (2) | 2023.06.25 |
| 내신용 - 고차식 나머지 문제 선별 (0) | 2023.05.13 |