두 일차식의 곱으로 인수분해 되는 유형을 풀 때, 저는 판별식의 판별식(D of D)을 쓰기보다는, 그냥 상수항 인수분해+전체 인수분해로 대부분 푸는 편입니다. 대부분의 경우 이게 더 간단하거든요.
그렇지만 가끔 판별식 쓰는 경우가 더 편한 경우도 있어, 오늘 문제 하나 갖고 왔습니다.

문제

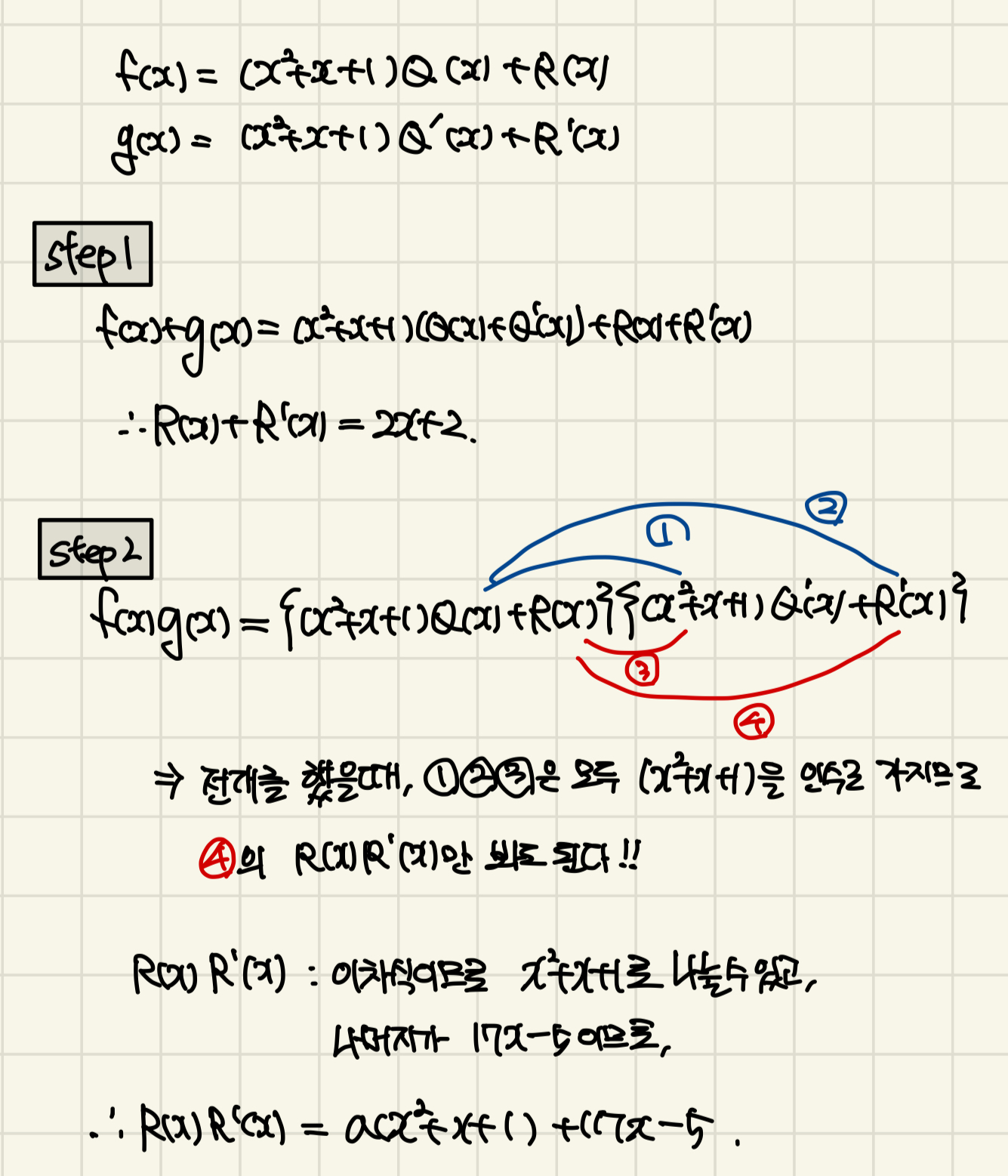
* 사실 이 부분 공부를 많이 한 학생들은 f(x), g(x)를 다 쓰지 않아도, 나머지 정리 바로 써서
R(x)+R '(x) = 2x+2,
R(x)R '(x)=a(x^2+x+1)+17x-5
Step3로 바로 넘어가셔도 됩니다.


우리가 구하는 R(x), R'(x)가 일차식이므로, 구한 해에 근호가 있으면 안되겠죠..?

여기서 D'이라고 쓴 판별식은 원래 t로 세운 이차방정식의 판별식 D/4의 판별식입니다.
이걸 보통 판별식의 판별식 (D of D)라고 불러요.
그래서 일차식 둘로 인수분해 되는 경우에는, 한 문자로 정렬해서 D of D =0으로 바로 푸셔도 됩니다.
사실 저는 복잡한 식의 인수분해를 많이 연습하면 이게 바로 되는 경우가 많아서, 저는 이 문제도 그렇게 풀 수 있을 거라고 생각했어요.

그런데 아무리 정수 조건이 있어도,
미지수 5개, 식5개는 그냥 손이 거부하더라고요.. 하나씩 소거해서 나가면 될 거 같긴 하지만, 할 자신이 없어서 패스...
문제2
x, y에 대한 이차식 x²-y²-2x-ky-k-2가 x, y의 두 일차식의 곱으로 인수분해되도록 하는 모든 실수 k의 값을 구하시오.
정답 : 6, -2
이 참에 D of D도 익혀두시고,
일차식의 곱으로 바로 푸는 문제는 다음에 예제와 같이 여럿 수록해볼게요 :-)
'고등수학 (2015 개정 교육과정) > 고등수학(상)' 카테고리의 다른 글
| 인수분해 - 공통부분 중 상수항 치환하는 문제 (0) | 2024.12.09 |
|---|---|
| [내신] 나머지 정리 - 낯선 문제 모음 (1) | 2024.04.20 |
| [도형의 이동] 평행이동 대칭이동 최단거리 고난도 문제 (0) | 2023.09.24 |
| 도형의 이동 - 선대칭 최단거리 푸는 방법 (거리합의 최솟값) (0) | 2023.07.15 |
| 아폴로니우스의 원 - 두 점으로부터 거리의 비가 같은 점의 자취 (2) | 2023.06.25 |