내외분점이나 무게중심 등을 이용하여 도형의 넓이비를 묻는 문제를 풀어보도록 할게요.

이런 유형을 풀기 전 중학교 2학년 때 배운 높이가 같은 두 삼각형의 넓이비를 알고 계셔야 합니다.

내외분점 위치만 잘 표기하고, 문제에 따라 차분히 도형을 제대로 그리기만 한다면 어렵지 않게 풀 수 있습니다.
같이 풀어보도록 해요 :-)
예제 1
평행사변형 ABCD의 대각선 BD의 중점을 M, △ABD의 무게중심을 G라고 하고, 선분 GD를 2:3으로 외분하는 점을 E라고 하자. △AED의 넓이는 △DGM의 넓이의 k배이다. 이때 k를 구하고 그 풀이과정을 서술하시오.
설명대로 그림을 그려봅시다.
평행사변형 ABCD

대각선 BD의 중점을 M

△ABD의 무게중심을 G라고 하고,

선분 GD를 2:3으로 외분하는 점을 E라고 하자.
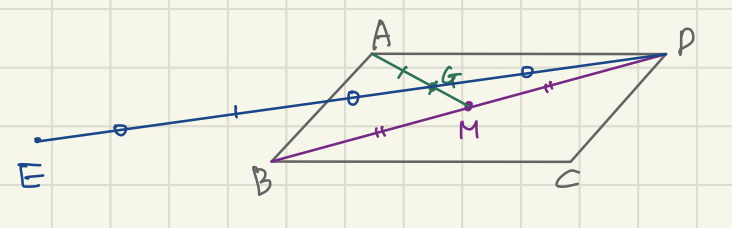
△AED의 넓이 = k△DGM의 넓이
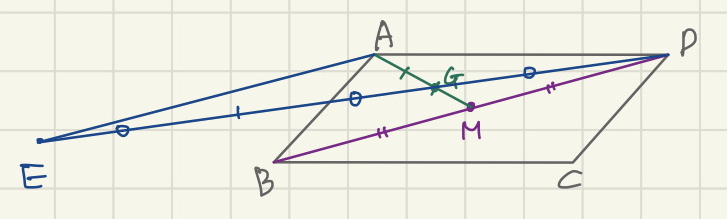
더 작은 △DGM의 넓이를 S라고 두자.

△AGD의 넓이 = 2△DGM의 넓이 = 2S

△AED=3△AGD의 넓이 = 6S

따라서 k=6입니다.
기출 문제
고1 2015년 9월 학력평가 #28
삼각형 ABC에서 선분 BC를 1:3으로 내분하는 점을 D, 선분 BC를 2:3으로 외분하는 점을 E, 선분 AB를 1:2로 외분하는 점을 F라 하자. 삼각형 FEB의 넓이는 삼각형 ABD의 넓이의 k배이다. 이때, 상수 k의 값을 구하시오.
이것도 조건에 맞게 그림을 잘 그려봅시다.!
삼각형 ABC에서

선분 BC를 1:3으로 내분하는 점을 D,

선분 BC를 2:3으로 외분하는 점을 E,

선분 AB를 1:2로 외분하는 점을 F라 하자.

△FEB = k△ABD
더 작은 △ABD=S라 두자.

BD:DC = 1:3이므로 △ADC=3S

FA:AC=1:1이므로 △FAB=4S

EB:BC=2:1이므로 △FEB = 16S


혹시나 내외분점이 약한 친구들은 시험보기 전에 꼭 아래 내용도 복습하고 가도록 해요.
길이비를 내/외분점으로 고치는 방법 (선분의 내분점,외분점 활용)
오늘은 선분의 내분점/외분점 문제 중 가장 많이들 헷갈려하는 선분의 길이비를 다룰까 합니다. 내분, 외분에 대한 정확한 정의와 개념이 없으면 풀기가 힘든 유형이죠. 공식보다는 선분을 m:n으
ladyang86.tistory.com
'고등수학 (2015 개정 교육과정) > 고등수학(상)' 카테고리의 다른 글
| 파푸스의 정리 (중선 정리 증명 + 응용 문제풀이) (1) | 2022.08.20 |
|---|---|
| x축과 y축에 동시에 접하는 원 쉽게 푸는 법 (0) | 2022.06.26 |
| 실수 조건 부정 방정식 연습하기 (완전제곱식, 판별식 D 이용) (0) | 2022.05.18 |
| [나머지 정리] 이차식, 완전제곱식으로 나눈 나머지 (0) | 2022.04.09 |
| 대칭이동 - 선대칭 직선 기울기가 +1, -1일 때 빨리 하는 방법 (2) | 2022.03.06 |