동경의 위치관계
혹시 이상한 공식 같은 거(?) 외워서 풀려는 학우 여러분은 없겠죠?
오늘은 이해를 기반으로 한 동경의 위치관계를 총정리 해볼까 합니다.

순서는 아래와 같습니다.
1. 그래프를 그린다.
(이 때 동경은 최대한 안예쁘게(?) 그린다.)
2. 두 동경을 적절하게 더하거나 빼서
특수각을 만든다.
(0˚, 90˚, 180˚, 270˚ 등등..)
3. 식을 정리 후,
범위에 맞게 n을 대입해준다.
그래서 이 순서에 맞게, 두 동경이 일치하는 경우, x축 대칭인 경우, y축 대칭인 경우, 원점 대칭인 경우, y=x 대칭인 경우로 전부 다 풀어보면서 하나씩 익혀보도록 합시다.
문제1
각 θ를 나타내는 동경과 각 5θ를 나타내는 동경이 일치한다. 이러한 각θ를 구하여라.
(단 0º<θ<270º)
1. 우선 그림을 그려봅니다.

2. 두 각을 뺐을 때 0이 나오는 군요.
그럼 5θ-θ=0º라고 세우면 되나요?
몇바퀴 돌다 온 동경인지 모르기에
반드시 뒤에 360 ºn을 붙여주셔야 합니다.
즉 5θ-θ=0º+360ºn
4θ=360ºn
θ=90ºn이 되네요.
3. n은 정수이므로 차례대로 숫자를 넣어,
범위에 맞는 각을 찾아줍시다.
θ=90ºn이므로
θ= 90º, 180º가 됩니다.
문제2
각 2θ를 나타내는 동경과 각 4θ를 나타내는 동경이 x축에 대하여 대칭일 때, 각θ의 크기를 구하여라.
(단 180º<θ<270º)
1. 우선 그림을 그려봅니다.
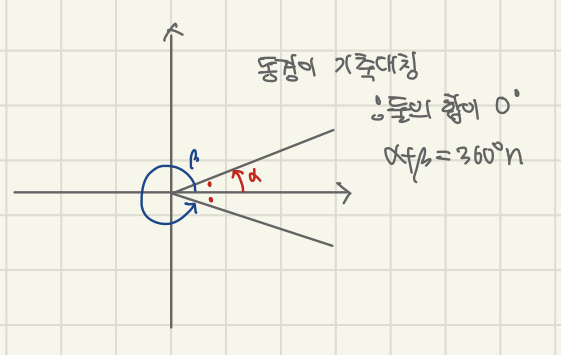
2. 두 각을 더하면 0º가 나오는 군요.
그럼 2θ+4θ=0º라고 세우면 되나요?
몇바퀴 돌다 온 동경인지 모르기에
반드시 뒤에 360 ºn을 붙여주셔야 합니다.
즉 2θ+4θ=0º+360ºn
6θ=360ºn
θ=60ºn이 되네요.
3. n은 정수이므로 차례대로 숫자를 넣어,
범위에 맞는 각을 찾아줍시다.
θ=60ºn이므로 θ=240º입니다.
문제3
각 2θ를 나타내는 동경과 각 4θ를 나타내는 동경이 y축에 대하여 대칭일 때, 각θ의 크기를 구하여라.
(단 0º<θ<180º)
1. 우선 그림을 그려봅니다.

2. 두 각을 더하면 180º이 나오는 군요.
그럼 2θ+4θ=180º라고 세우면 되나요?
몇바퀴 돌다 온 동경인지 모르기에
반드시 뒤에 360 ºn을 붙여주셔야 합니다.
즉 2θ+4θ=180º+360ºn
6θ=180º+360ºn
θ=30º+60ºn이 되네요.
3. n은 정수이므로 차례대로 숫자를 넣어,
범위에 맞는 각을 찾아줍시다.
θ=30º, 90º, 150º가 됩니다.
문제4
각 2θ를 나타내는 동경과 각 5θ를 나타내는 동경이 원점에 대하여 대칭일 때, 각θ의 크기를 구하여라.
(단 0º<θ<360º)
1. 우선 그림을 그려봅니다.
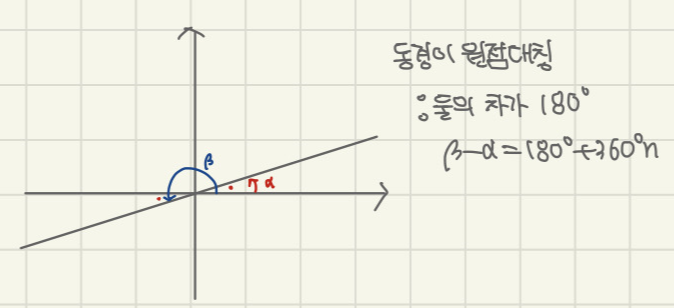
2. 두 각을 뺐을 때 180º가 나오는 군요.
그럼 5θ-2θ=180º라고 세우면 되나요?
몇바퀴 돌다 온 동경인지 모르기에
반드시 뒤에 360 ºn을 붙여주셔야 합니다.
즉 5θ-2θ=180º+360ºn
3θ=180º+360ºn
θ=60º+120ºn이 되네요.
3. n은 정수이므로 차례대로 숫자를 넣어,
범위에 맞는 각을 찾아줍시다.
θ=60º, 180º, 300º
문제4'
각θ를 나타내는 동경과 각 6θ를 나타내는 동경이 일직선 위에 있고 방향이 반대일 때, 각 θ의 크기를 구하여라.
(단 0º<θ<180º)
1. 우선 그림을 그려봅니다.

그림으로 그려보면,
사실 표현만 다를 뿐이지,
두 동경은 원점 대칭임을 알 수 있습니다.
2. 두 각을 뺐을 때 180º가 나오는 군요.
그럼 6θ-θ=180º라고 세우면 되나요?
몇바퀴 돌다 온 동경인지 모르기에
반드시 뒤에 360 ºn을 붙여주셔야 합니다.
즉 6θ-θ=180º+360ºn
5θ=180º+360ºn
θ=36º+72ºn이 되네요.
3. n은 정수이므로 차례대로 숫자를 넣어,
범위에 맞는 각을 찾아줍시다.
θ=36º, 108º가 됩니다.
문제5
각 2θ를 나타내는 동경과 각 4θ를 나타내는 동경이 직선 y=x에 대하여 대칭이다. 이러한 각θ중 예각을 구하여라.
1. 우선 그림을 그려봅니다.
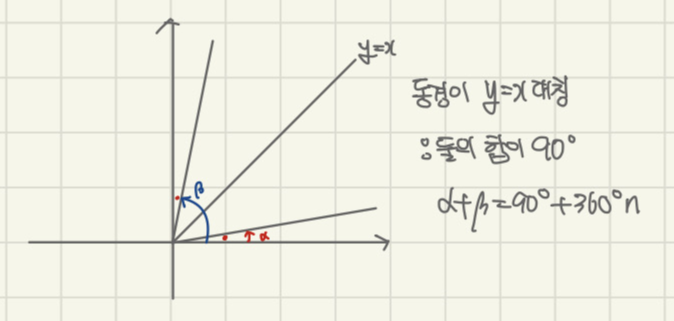
2. 두 각을 더하면 90º가 나오는 군요.
그럼 2θ+4θ=90º라고 세우면 되나요?
몇바퀴 돌다 온 동경인지 모르기에
반드시 뒤에 360 ºn을 붙여주셔야 합니다.
즉 2θ+4θ=90º+360ºn
6θ=90º+360ºn
θ=15º+60ºn이 되네요.
3. n은 정수이므로 차례대로 숫자를 넣어,
범위에 맞는 각을 찾아줍시다.
θ=15º, 75º입니다.
다시 복습해봅시다.
순서는 아래와 같습니다.
1. 그래프를 그린다.
(이 때 동경은 최대한 안예쁘게(?) 그린다.)
2. 두 동경을 적절하게 더하거나 빼서
특수각을 만든다.
(0˚, 90˚, 180˚, 270˚ 등등..)
3. 식을 정리 후,
범위에 맞게 n을 대입해준다.
문제 풀 때 주의사항이 있습니다.
1. 동경은 최대한 안 예쁘게(?) 비대칭적으로 그려주세요.

: 제자 중, y축 대칭인 동경을 그린 다음, 그림으로 봤을 때 둘의 차가 90º라고 식을 세운적이 있답니다. 이런 실수를 안 하려면 최대한 비대칭적으로 동경을 그려주세요.
2, 구하는 동경이 몇 사분면에 있건, 그림은 헷갈리지 않게 1사분면에 그려서 풀어주세요.
예를 들어, 동경이 2사분면에 있는 x축 대칭이라고 해서, 꼭 아래와 같이 정확하게 그릴 필요는 없어요.

물론 이것도 그리고 나면 두 동경의 합이 0˚게 보이긴 하지만, 어차피 그림을 그려서 개형을 파악하는게 더하는지/빼는지, 특수각이 뭐가 나오는지 알기 위한거라 관계식은 결국 동일하게 나온답니다 :-)
그럼 가볍게 문제 한 번 풀어볼까요?
문제
두 각 α , β에 대한 설명으로 옳은 것만을 <보기>에서 있는 대로 고른 것은?

정답 : ㄱ,ㄷ
ㄱ. o
ㄴ. x : α +β에 대한 설명이다.
ㄷ. o
ㄹ. x : α -β에 대한 설명이다.
수학은 이해해서 풀면 쉽답니다. 내용 잘 숙지하셔서 여러분의 중간고사에 좋은 결과가 있길 바랄게요!
위 포스팅한 내용으로 강의한 영상도 유튜브에 업로드 하였으니, 눈으로만 봐서 잘 모르겠다-하는 분들은 영상도 같이 시청해주시면 됩니다!
'고등수학 (2015 개정 교육과정) > 수학1' 카테고리의 다른 글
| [지수] 거듭제곱근 실근의 개수 (내신 선별) (0) | 2022.04.17 |
|---|---|
| 지수 - 곱셈 공식의 변형, 치환해서 풀기 (0) | 2022.04.16 |
| 지수/로그 방정식 치환해서 푸는 유형 (0) | 2022.04.01 |
| 거듭제곱근 정의 관련 문제 모음 (0) | 2022.03.30 |
| 점화식 an+1=pan+q꼴 일반항 알고리즘 및 예제 (0) | 2022.02.06 |