명제가 참인지 거짓인지는
진리 집합간의 포함관계로
판단하시면 됩니다.
즉 P⊂Q이면
p⇒q인 것이죠.
부등식이나 방정식 역시
이러한 방법으로 나타내면 좀 더 편하게
판단할 수 있습니다.

문자가 a,b인 경우도 마찬가지인데,
우리는 항상 축을 x,y로 썼으니
오늘 실린 모든 예제는
다 x,y라는 문자만 사용할거에요.
혹시나 다른 문자가 나오더라도
문자 바꿔서 그리시면 됩니다.
예제1
p : x=0이거나 y=0이다.
q : x²+y²=0이다.
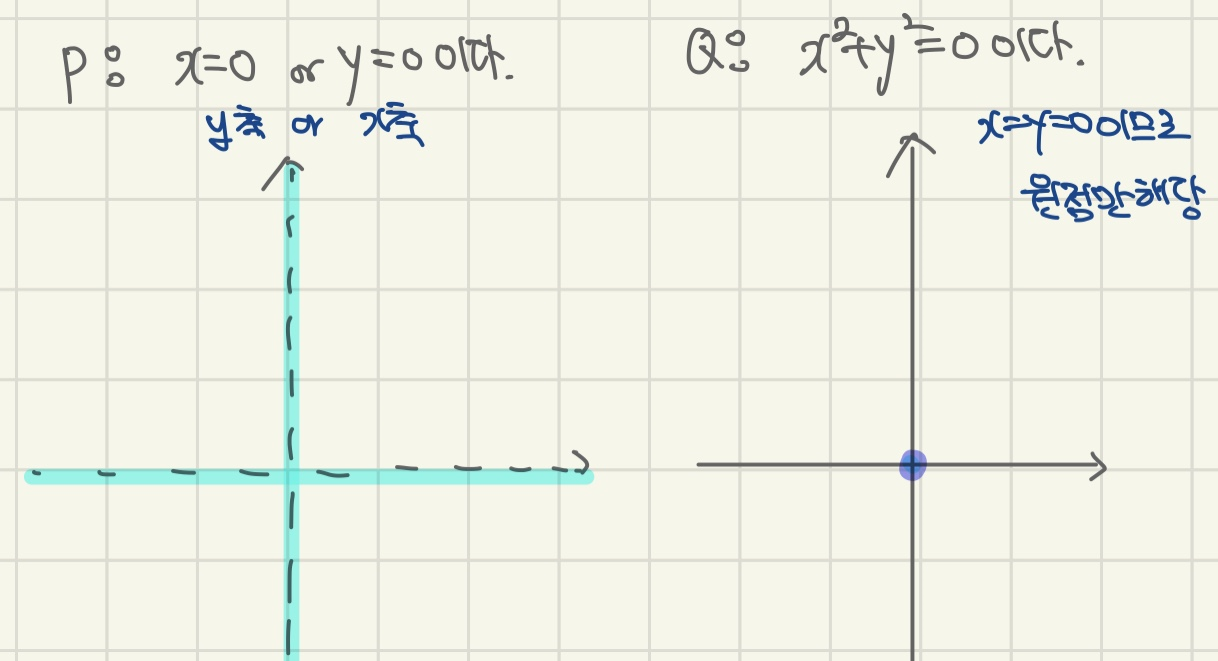
x=0은 y축, y=0은 x축이고
or는 합집합이므로 둘다 그려주면 됩니다.
진리집합을 다 표시한 다음에는
포함관계를 살펴보시면 돼요!

예제2
p : x=y
q : x²=y²
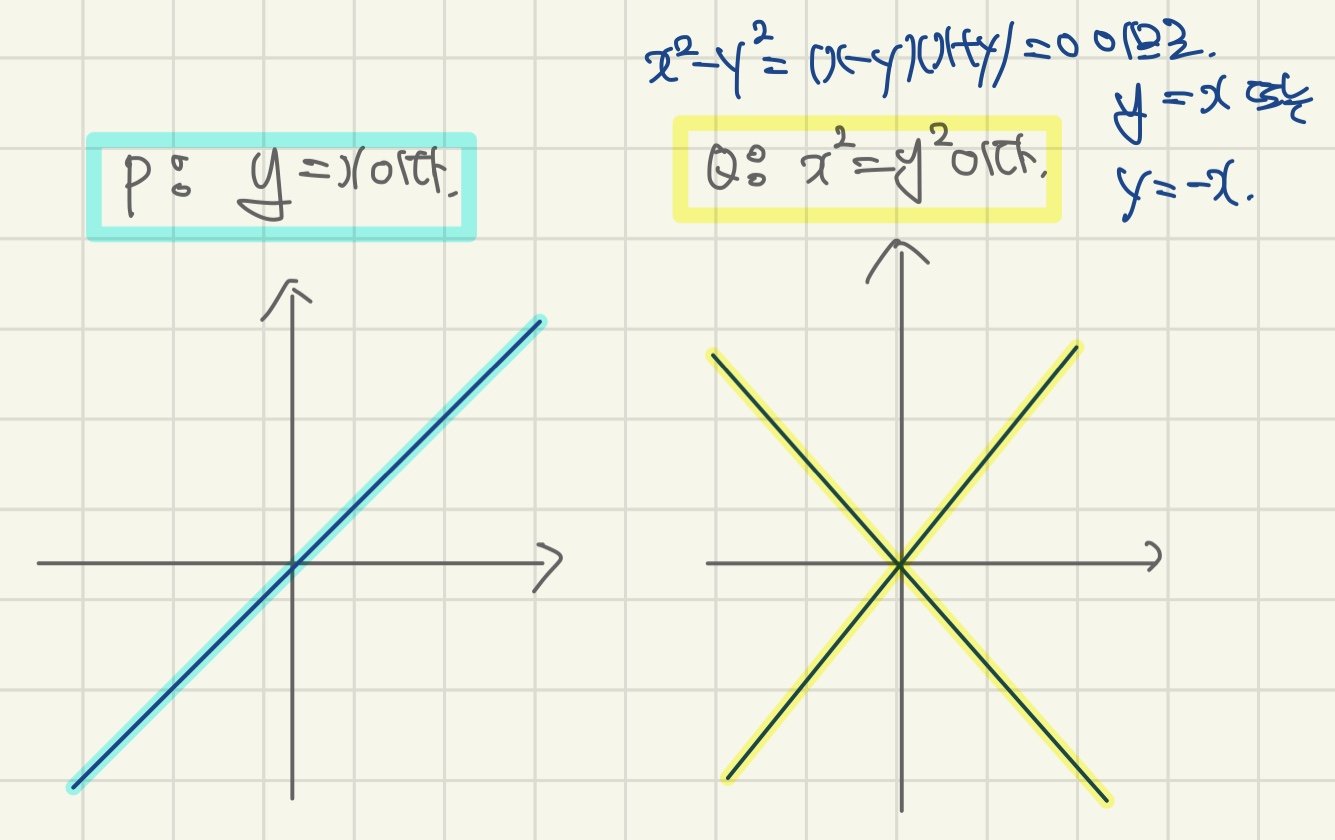
이건 직선으로 나타내시면 됩니다.
특히 q의 경우에는 인수분해가 되므로
직선을 2개 그리시면 돼요.
이제 진리집합을 표기했으니
포함관계를 살펴보시면 됩니다.

예제3
p : x+y≥2
q : x≥1 이고 y≥1이다.
r : xy>1이다.

부등식의 영역으로 표시하시면 됩니다.
우리가 일반적으로 그리는 도형이
등호가 성립하는 부분이므로
그 윗부분/아랫부분에 점을 찍어서
식에 넣었을 때 누가 큰지를 살펴보시면 돼요.

마지막 r 조건은 조금 까다롭습니다.
일단 나눗셈을 할 때 부호에 따라서
부등호의 방향이 달라지기 때문이죠.

세 조건을 살펴보시면,
Q⊂P이고, Q⊂R이지만
P와 R은 서로 포함이 안되는
부분이 있기 때문에
어떤 조건이라고 말할 수 없습니다.
예제4
두 실수 x, y에 대하여
다음 두 명제가 모두 참이 되도록 하는
정수 k의 개수는?
(가) x²+y ²-2x+4y+k ²+2k-3=0을
만족하는 x, y가 존재한다.
(나) x+y<4이면 x<k 또는 y<6이다.

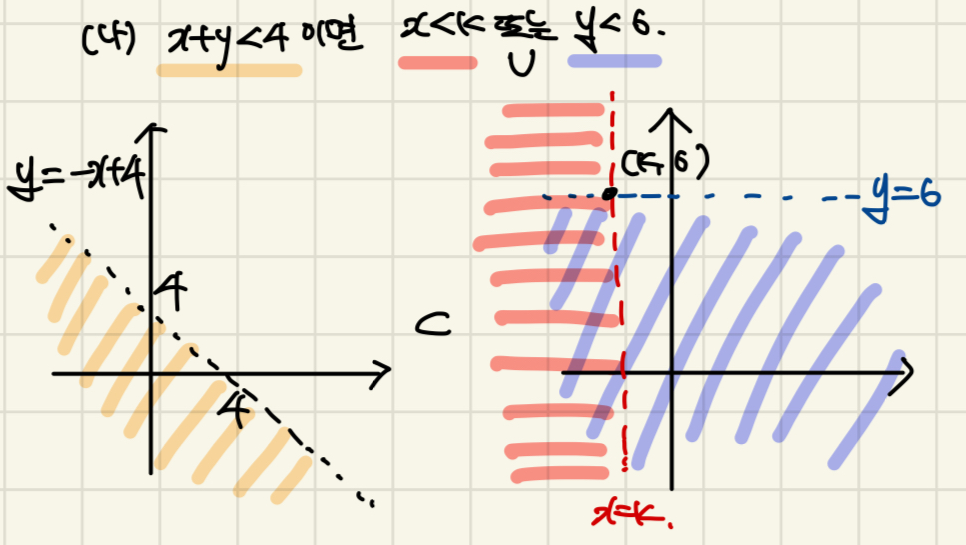
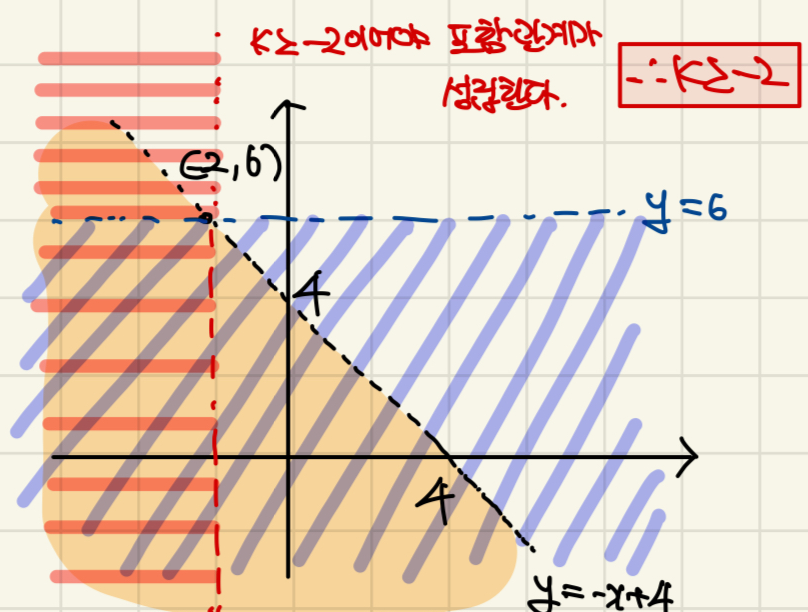

정답 : 5
만약 문자가 ab>1처럼 x,y가 아닐 경우
x,y로 바꿔서 풀던가
아님 축을 a축, b축을 기준으로 두면
동일하게 그래프를 그릴 수 있어요.
익숙하지 않은 부분이라
머리로만 참/거짓을 판단하셨다면
이렇게 좌표평면에 그리시는 게
많은 도움이 되실 거에요!
'고등수학 (2015 개정 교육과정) > 고등수학(하)' 카테고리의 다른 글
| 명제의 거짓 반례 조건 (0) | 2022.02.19 |
|---|---|
| 우함수, 기함수 곱/합성 성질 정리 (0) | 2021.11.13 |
| 유리함수의 평행이동 쉽게 찾는 법 (0) | 2021.09.09 |
| 집합의 정의 + 집합을 원소로 갖는 집합 문제 모음 (0) | 2021.07.12 |
| 고1이 풀만한 함수방정식 문제 (연립방정식으로 풀이) (0) | 2021.01.22 |