오늘은 고1이 풀어볼만한 함수방정식을 몇 개 갖고 와봤습니다.

함수방정식은
함수 자체를 근으로 하는
방정식을 말합니다.
얼핏 보기엔 굉장히 힘들어 보이지만,
푸는 방식은 연립방정식과 비슷해요.
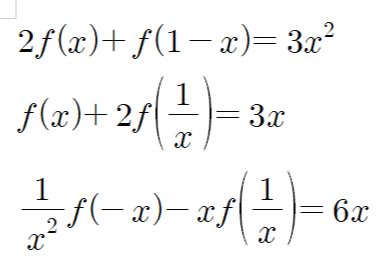
푸는 방법은 다 같습니다.
1. 함숫값에 들어가는
두 방정식의 문자가
같게 만들어 줍니다.
2. 연립방정식처럼
가감법을 이용하여
풀어줍니다.
그럼 하나씩 풀어볼까요?
예제1
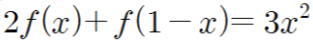
함숫값에 들어가는 두 문자는
x와 1-x죠.
둘을 바꿔서 넣어주면 됩니다.
즉 x 대신 1-x를 넣는거죠.
그럼 1-x는 x가 되겠죠?

식을 정리해서
f(x)는 f(x)끼리,
f(1-x)는 f(1-x)끼리 오도록
세로식을 정리해줍니다.

우리가 구하는 건 f(x)이니까,
가감법을 사용하여
f(1-x)를 없애주면 됩니다.
함수 자체를 다루는 거라,
식이 잘 와닿지 않는다면,
치환해서 푸셔도 괜찮습니다.
보기쉽게
f(1-x)=A로, f(x)=B로 치환해서
연립방정식을 풀어보았습니다.
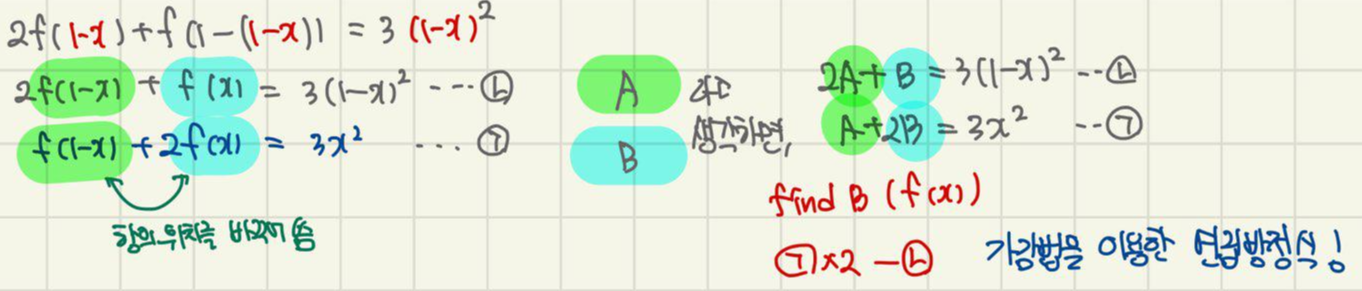
함수 자체를 하나의 문자로 생각해서
풀면 됩니다.

참 쉽죠?ㅎㅎ
예제2

이번엔 함수에 들어가는 변수가
x와 1/x입니다.
이 둘도 바꾸어서 넣어줍시다.
x 대신 1/x를 넣으면,
1/x은 x가 되는군요!
이후의 풀이는
가감법을 이용하여
아래와 같이 푸시면 됩니다.

예제3

마지막 문제입니다.
앞의 두 문제보다는 어려워 보이나요?
이 문제 역시 f 안의 변수에 집중합니다.
-x와 1/x이군요.
이 둘을 바꾸어서 넣어봅시다.
-x 대신 1/x을 넣을 겁니다.
즉, x 대신 -1/x를 넣는 모양이죠.
가감법을 사용할 때,
양변에 x를 곱해서 더하면 됩니다.

사실 고1은 함수방정식을 이용하여, 함수를 직접 구하기보다는, 특정 함숫값을 구하라는 문제가 많이 나오는 편이긴 합니다.
그렇지만 제 경험상 학생들 대부분이 넣어야 할 '적절한 값'을 못 찾는 경우가 상당히 많아서.. 아에 함수 자체를 구하는 법을 포스팅 해봤네요.ㅎㅎ
유용하게 사용하시길 바라며 오늘의 포스팅 마칩니다.^^
'고등수학 (2015 개정 교육과정) > 고등수학(하)' 카테고리의 다른 글
| 유리함수의 평행이동 쉽게 찾는 법 (0) | 2021.09.09 |
|---|---|
| 집합의 정의 + 집합을 원소로 갖는 집합 문제 모음 (0) | 2021.07.12 |
| 서로 다른 주사위 경우의 수 문제 총정리 (합,차, 그 외 기타) (0) | 2020.12.13 |
| 유리함수 절댓값 그래프 그리기 (0) | 2020.12.10 |
| [경우의 수] 시험 꿀팁 교란순열 (완전순열) (0) | 2020.12.05 |