집합의 정의
집합 : 어떤 조건에 의하여 그 대상을 명확하게 구분할 수 있는 것들의 모임.
여기서 명확하게 구분할 수 있다는 말은, 누가 들어도 이견이 없이 명확하다는 뜻입니다.
ex) 축구를 잘하는 사람들의 모임
잘 한다는 기준은 사람마다 다릅니다.
ex2) 월드컵 국가 대표 선수들의 모임
누가 봐도 명확하죠.
예제
다음 중 집합인 것에는 o표, 집합이 아닌 것에는 x 표를 하여라.
1. 작은 짝수의 모임
2. 다리가 4개인 동물들의 모임
3. 7보다 작은 홀수의 모임
4. 날개가 있는 동물들의 모임
5. 우리나라에서 인구가 많은 도시의 모임
6. 꽃받침이 있는 식물들의 모임
7. 키 큰 사람의 모임
8. 자연수에서 큰 수의 모임
9. 우리반에서 키가 가장 큰 사람의 모임
10. 아름다운 꽃들의 모임.
해설
1. 작은 짝수의 모임
: x, 작다는 기준은 주관적인 것이므로 집합이 될 수 없습니다.
2. 다리가 4개인 동물들의 모임
: o, 다리가 4개라고 명시되어 있으므로 집합입니다.
3. 7보다 작은 홀수의 모임
: o, 1,3,5 세 개가 해당 되겠네요.
4. 날개가 있는 동물들의 모임
: o
5. 우리나라에서 인구가 많은 도시의 모임
: x, 많다는 기준은 주관적입니다.
그러나 여기서 우리나라에서 가장 인구가 많은 도시의 모임을 물어본다면, 이것은 집합입니다.
우리나라에서 가장 인구가 많은 도시는 서울 하나뿐이기 때문이죠.
6. 꽃받침이 있는 식물들의 모임
: o
7. 키 큰 사람의 모임
:x, 크다는 기준 역시 주관적이죠?
8. 자연수에서 큰 수의 모임
:x, 크다는 기준은 객관적이지 않습니다.
9. 우리반에서 키가 가장 큰 사람의 모임
:o, 모임이라고 하니 여러명 있어야 할 것 같지만, 가장 키 큰 사람 한 명만 포함되는 집합입니다.
10. 아름다운 꽃들의 모임.
:x, 아름답다는 기준은 사람마다 다르죠.
어떤 게 집합인지 이제 잘 구분이 되실까요?
원소
집합을 이루고 있는 대상 하나하나를 그 집합의 원소라고 합니다.
위에서 살펴본 집합 중
7보다 작은 홀수의 모임은 집합이고, 여기의 구성원들은 1,3,5가 되죠. 이 때 이 1,3,5를 집합의 원소라고 합니다.
일반적으로 집합은 알파벳 대문자 A,B,C, ... 로 나타내고, 원소는 알파벳 소문자 a,b,c, ...로 나타냅니다.
a가 집합 A의 원소일 때, a는 집합 A에 속한다고 하고, 기호로 a∈A와 같이 나타냅니다.

여기서 기호 ∈는 원소를 뜻하는 Element의 첫 글자 E의 모양을 기호화한 것입니다.
a가 집합 A의 원소가 아닐 때, a는 집합 A에 속하지 않는다고 하고,기호에 사선을 그어 아래와 같이 나타냅니다.

정리하자면

집합을 나타내는 방법 3가지
1. 원소나열법
집합에 속하는 모든 원소를 { } 안에 나열하는 방법.
원소들끼리의 구분은 ,를 통해 나타냅니다.
{원소1, 원소2, 원소3}
주의!
ㅇ같은 원소는 중복하여 쓰지 않습니다.
학번 1224에 쓰인 숫자의 집합은 {1,2,2,4}가 아닌 {1,2,4}로 씁니다.
ㅇ원소의 순서는 상관 없습니다. (나열하는 순서는 바꾸어도 됩니다.)
ex) 요일
= {월,화,수,목,금,토,일}
= {일,월,화,수,목,금,토}
ㅇ원소가 많고 일정한 규칙에 따라 원소를 차례로 나열할 수 있을 때에는 '...'을 사용하여 일부를 생략하여 나타낼 수 있습니다.
ex) 집합 B가 1부터 10까지의 자연수일 때
B={1,2,3, ..., 10}으로 표현 가능
2. 조건제시법
집합의 원소들이 공통으로 가지는 성질을 제시하여 집합을 나타내는 방법.
어떤 집합에 속하는 원소가 만족시켜야 하는 조건을 f(x)라고 할 때, {x|f(x)}로 표현.
ex) B={ x | 1≤ x ≤ 10, x는 자연수}와 같이 표현.
즉, {x|x가 만족시켜야 하는 조건}와 같은 형태로 제시합니다. 문자는 x가 아닌 y,z등 다른 문자를 써도 됩니다.
해석은 영어 어순과 동일하게 해석합니다.
집합의 원소는 x, 이 원소 x가 어떤 것인지에 대한 설명 부분이 f(x)로 뒤에 나오는 것이죠.
ex) 10의 양의 약수의 집합을 A라고 하면
A={1,2,5,10} 원소나열법
A={x|x는 10의 양의 약수} 조건제시법
실수, 유리수, 정수의 집합 등과 같이 원소의 개수가 무수히 많은 경우거나, 원소나열법으로 나타냈을 때 집합의 성격을 명확히 할 수 없을 때에는 원소나열법보다 조건제시법으로 나타내는 것이 명확합니다.
ex) A는 정수 전체의 집합이라고 해봅시다.
어떤 학생이 A={±1, ±2, ±3, ±4, ...} 이렇게 원소나열법으로 나열했다고 해봅시다.
음.. 아쉽게도 0을 빼고 썼군요. 이런 경우 원소나열법으로 쓰는 것보다, A={x|x는 정수}으로 나타내는 조건제시법이 훨씬 깔끔합니다. 물론 원소나열법으로도 정수를 A={..., -3, -2, -1, 0, 1, 2, 3, ...} 이런식으로 표현할 수도 있긴 합니다.
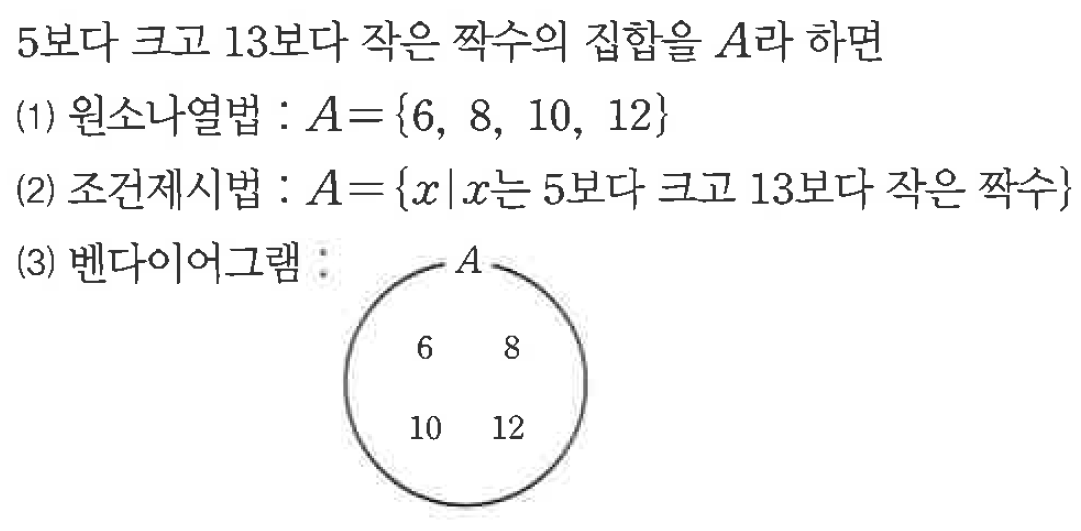
3. 벤다이어그램
집합을 원이나 직사각형등을 이용하여 그림으로 나타내는 방법
ㅇ 집합의 원소는 도형 안에 씁니다.
ㅇ 집합을 나타내는 기호는 도형 위에 씁니다.
ㅇ 벤다이어그램에서 원소들 간에 ,를 쓰지 않습니다. 원소는 따로 적당한 거리를 두고 써줍니다.
벤(Venn)은 이 그림을 처음으로 생각해 낸 영국의 논리학자의 이름이며,
다이어그램(diagram)은 그림표를 뜻하는 영어입니다.
원소의 개수에 따른 집합의 분류
원소가 유한개인 집합 : 유한집합
원소가 무한히 많은 집합 : 무한집합
원소가 하나도 없는 집합 : 공집합이라 하고, 기호로

라고 씁니다. 혹은 원소가 하나도 없는 집합이므로 { } 라고 쓸 수도 있습니다.
공집합의 경우 유한집합과 무한집합 중 유한집합으로 분류합니다.
유한집합 A의 원소의 개수를 기호로 n(A)와 같이 나타냅니다.
여기서 n은 개수를 뜻하는 영어 number의 첫글자에서 따온 기호랍니다.
A={1,2,3}일 때, n(A)=3
A가 공집합이면 n(A)=0
'고등수학 (2015 개정 교육과정) > 고등수학(하)' 카테고리의 다른 글
| [고1 함수] 일반적으로 정의된 함수 문제 (0) | 2024.11.09 |
|---|---|
| [집합] 약수, 배수 들어가는 문제 정리 (0) | 2023.10.08 |
| 대칭차집합 총정리 - 정의, 성질, 문제풀이 (0) | 2023.09.03 |
| [순열과 조합] nPr, nCr 성질 증명 및 예시 (서술형, 빈칸형 출제) (0) | 2022.11.13 |
| [경우의 수, 확률] 3의 배수 만들기 (3으로 나눈 나머지 이용) (2) | 2022.11.06 |