반응형
2022년 시행된 6월 모의고사 질문을 받았습니다. 학생이 해설지가 잘 이해가 안 된다고 갖고 왔는데, 저도 해설지 보다 혈압 올라서 작성하는 포스팅입니다.
저는 적분은 '함수값을 쌓는다'라고 표현을 합니다. 점이 쌓이면 선이 되고, 선이 쌓이면 면이 되듯이, 함숫값을 쌓으면 면적이 되죠. 이걸 이용하여 간단한 문제를 먼저 풀어볼게요.
예제
아래 그림은 이차함수 y=f(x)의 그래프이다. 함수 g(x)를
로 정의할 때, 함수 g(x)의 최솟값은?
정답 : g(2)
음수인 면적을 가장 많이 포함해야 하므로,
g(2)가 됩니다.
2023년 6월 20번
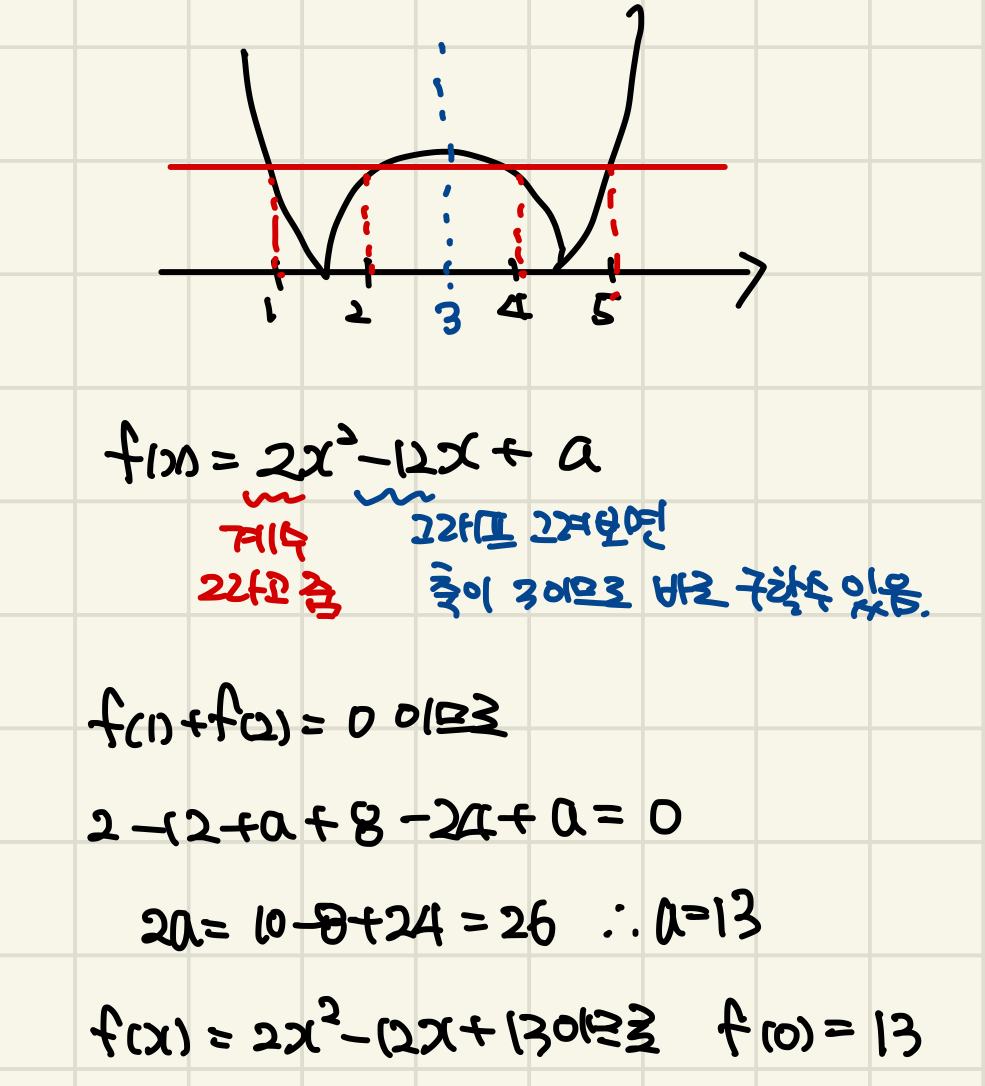
최고차항의 계수가 2인 이차함수 f(x)에 대하여 함수
는 x=1과 x=4에서 극소이다. f(0)의 값을 구하시오.
주어진 조건으로부터
f(x)가 어떻게 생겼을지를 고민해보세요.
아래와 같은 그래프가 나온다면 성공!
2024학년도 경찰대 #10
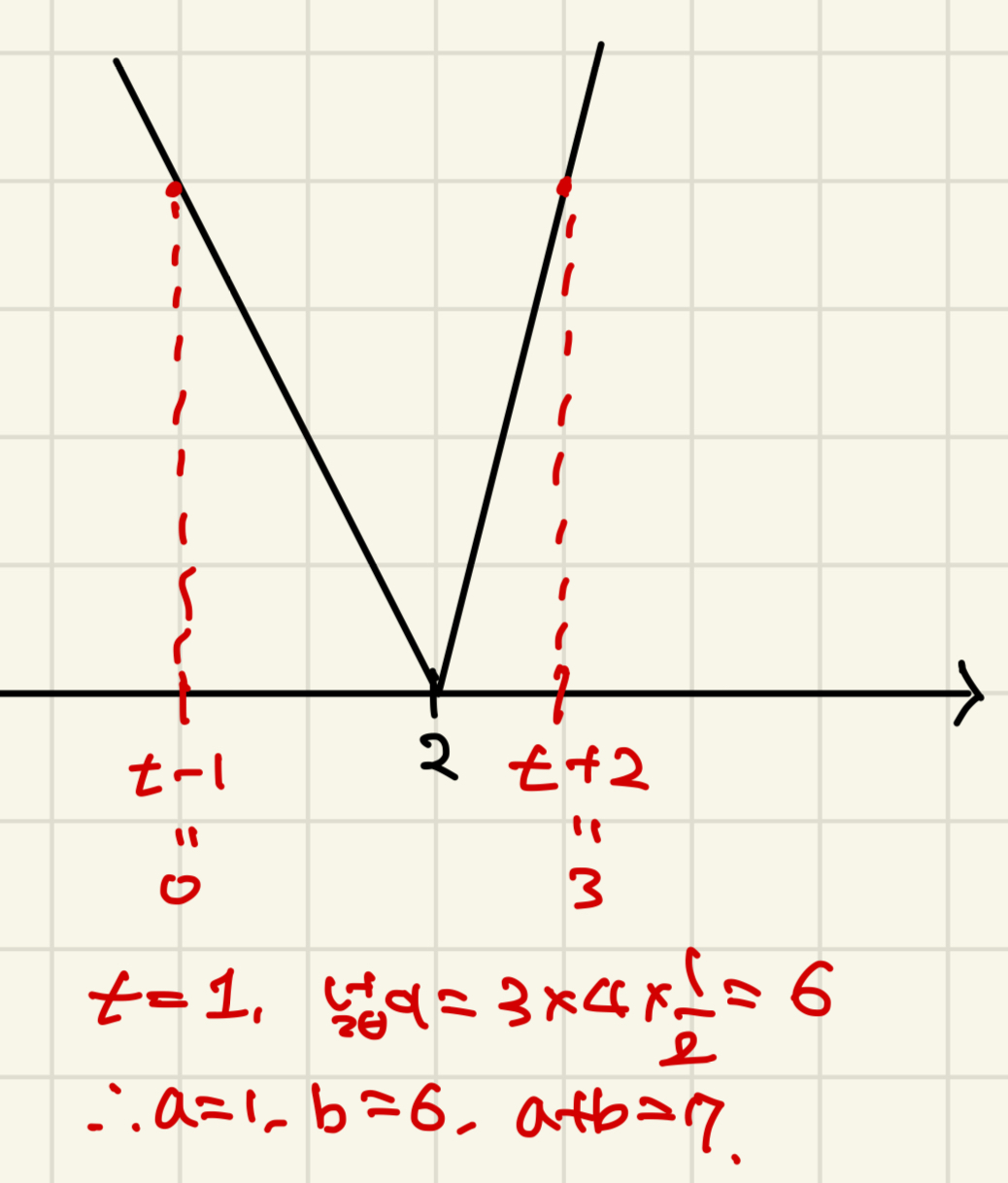
정답 : 7 (a=1, b=6)
이런 류의 문제가 좀 더 많았던 거 같은데, 틈틈이 추가해서 한 번 모아보도록 하겠습니다.!
반응형
'고등수학 > 수학2' 카테고리의 다른 글
| 미분계수 식변형 연습문제 (0) | 2024.04.14 |
|---|---|
| 적분 속도 문제 모음 (0) | 2023.12.02 |
| [삼차함수] 서로 다른 세 실근 => 극대x극소로 푸는 문제 (0) | 2023.11.10 |
| [함수 개형] 위로 볼록, 아래로 볼록 수식으로 나타내기 (0) | 2023.10.01 |
| 삼차함수 접선의 개수 문제 모음 (0) | 2023.08.27 |