반응형
최근 한양대 논술 기출 문제를 쭉 살펴보다, 경우의 수 입체 문제가 나왔길래 갖고 와봤습니다.
2024 한양대 자연계열 논술(오후1) 문제1
아래 그림은 크기가 같은 정육면체 25개를 가로로 5개, 세로로 5개씩 쌓아 만든 직육면체이다. 정육면체의 모서리를 따라 꼭짓점 P에서 꼭짓점 Q까지 최단거리로 이동할 때, 색칠된 정육면체의 꼭짓점을 지나지 않고 이동하는 경우의 수를 구하시오.

길찾기는 같은 것이 있는 순열로 푸는데, 이건 입체이므로 문자가 3개 필요합니다.
오른쪽을 R, 위를 U, 입체가 되기 위해 옆으로 한 칸 이동하는 걸 V라고 둘게요.
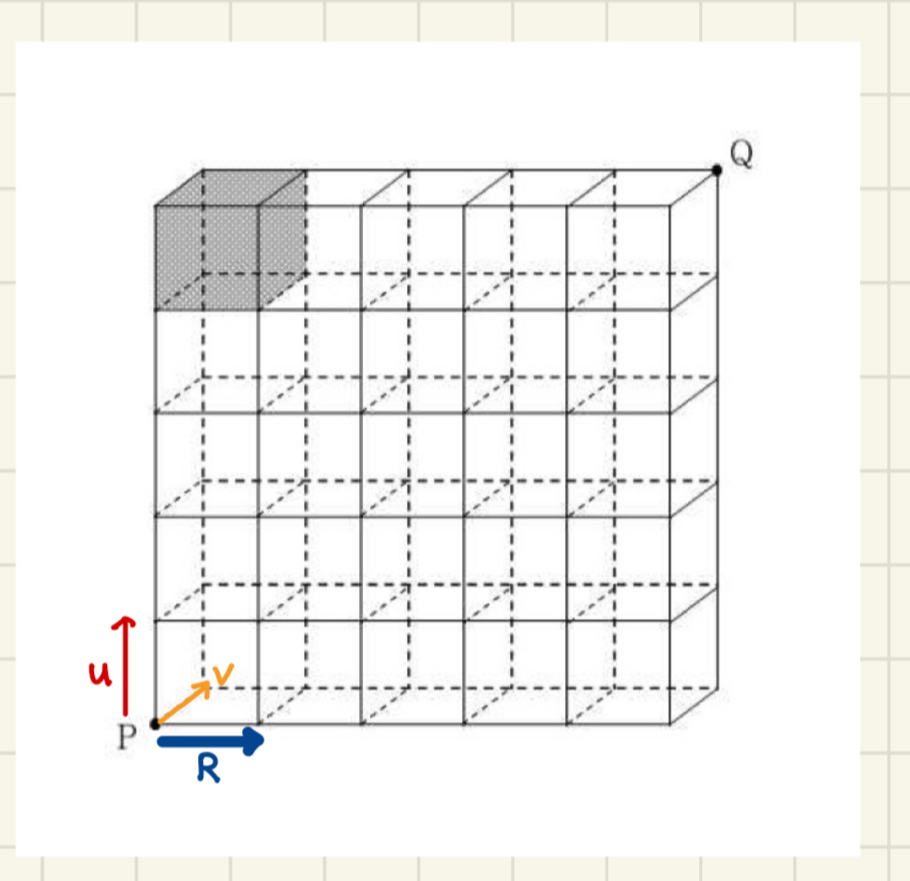
큰 구조는 다 전체 - 색칠한 부분을 지나는 경우를 제외할 겁니다.
Sol1) 평면으로 생각하고 나열한 다음, 입체가 되는 지점 끼워넣기.

우선 평면이라 생각하고 경우를 센 다음, P가 포함된 평면과 Q가 포함된 평면을 이어줄 구간이 어디인지 정하면 됩니다.
Sol2) 방법은 동일한데 입체를 직접 세서 뺌

(전체) - (색칠한 입체를 지나는 경우)
= (11! / 5!5!) - (42+120+24+100) = 2486
이게 오히려 직관적이긴 하네요. 어차피 EFGH로는 ABCD를 지나지 않고서는 갈 수 없으니 분류를 이렇게만 해줘도 충분한 것 같습니다.
반응형
'고등수학 (2015 개정 교육과정) > 확률과 통계' 카테고리의 다른 글
| [교재] 고2, 고3 확률과 통계 추천 문제지, 교재 (0) | 2025.12.11 |
|---|---|
| 중복조합 변수 치환 추가문제 (0) | 2024.05.16 |
| 처음으로 특정 지점에 도착하는 문제 모음 (0) | 2024.05.11 |
| 합성함수 원소의 개수 - 경우의 수, 확률 선별문항 (0) | 2024.04.06 |
| 통계적 추정, 표본평균 고난도 문제 모음 (수능+모의고사, 내신) (0) | 2023.06.10 |