유리함수의 그래프 어떤 형태든지 7초 만에 그리는 방법 오늘 배워보도록 할게요.
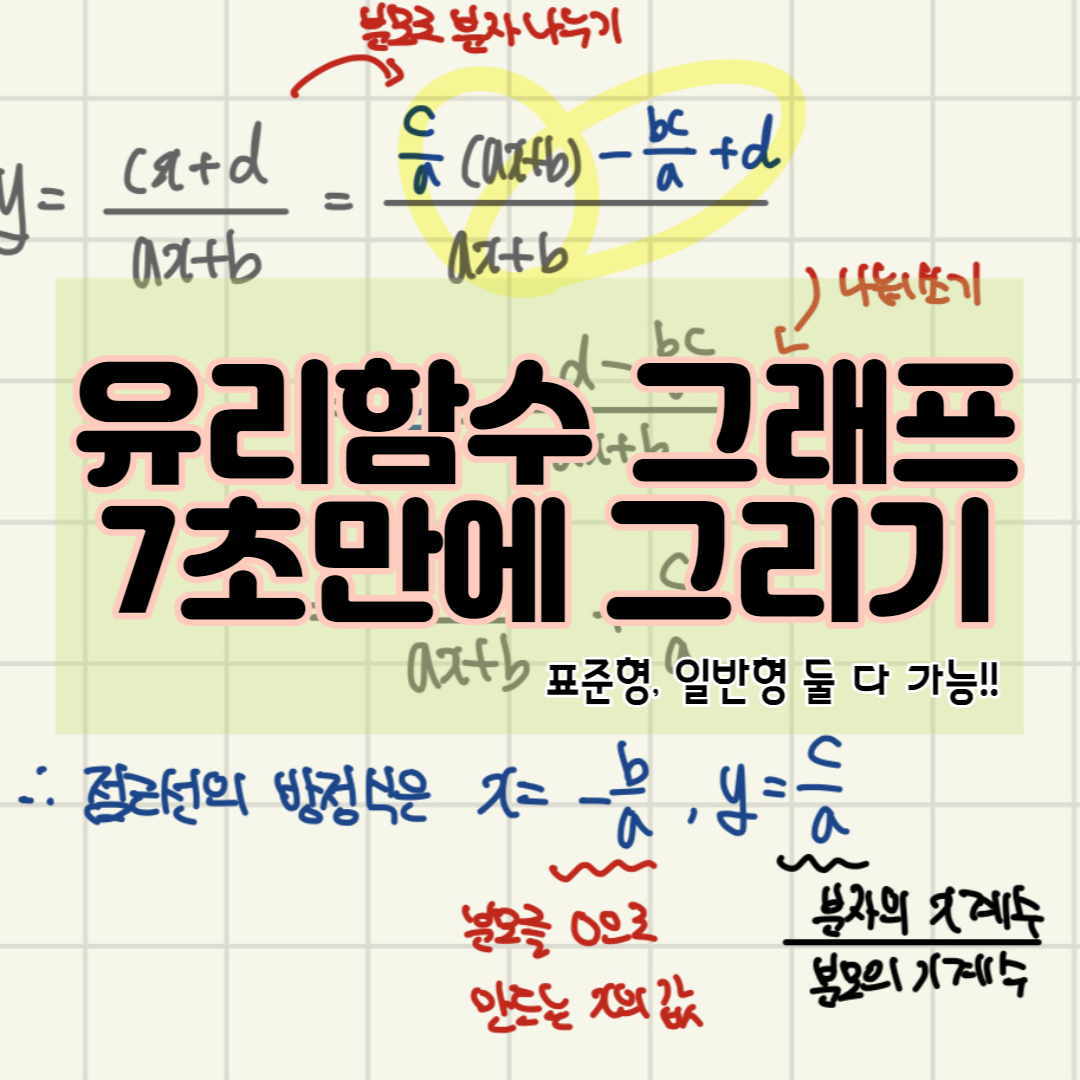
유리함수 그래프 그리는 방법
표준형, 일반형 상관없이 순서는 아래와 같습니다.
1. 점근선을 구한다.
2. 곡선이 지나는 한 점을 구한다. (주로 y절편 이용)
3. 점근선에 안 닿게 그래프를 잘 그려준다.
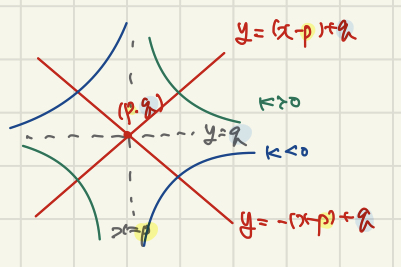
무엇보다도 유리함수의 그래프 특징을 익혀 두시는 게 가장 중요합니다.
유리함수 그래프는 선대칭인 동시에 점대칭이므로 그래프 성질만 똑바로 알아도 많은 문제를 금방 풀 수 있어요.

그리고 일반형의 경우에는,
아래와 같이 점근선의 방정식을 바로 찾을 수 있습니다.

정리하자면 아래와 같죠.

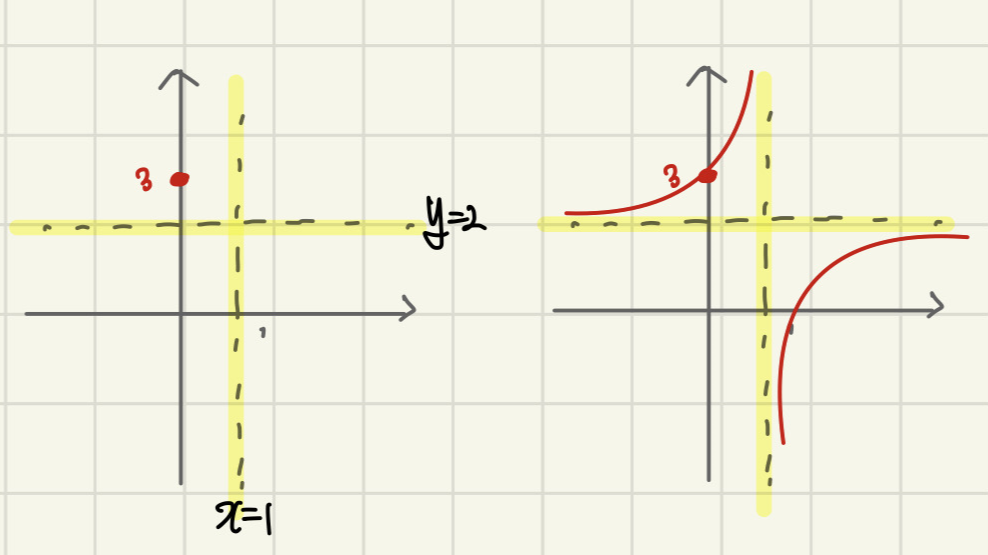
그럼 실제로 한 번 그려볼까요?

노란선에 닿지 않으면서 (점근선)
빨간 점을 지나는 (지나는 한 점)
유리함수의 그래프는 어떻게 생겼을까요?
아래와 같이 잘 이어주시면 됩니다.
한 문제만 더 연습해볼게요.
우선 점근선과 한 점을 찾습니다.

노란 선에 닿지 않으면서 (점근선)
빨간 점을 지나는 (지나는 한 점)
유리함수의 그래프는 어떻게 생겼을까요?
아래와 같이 잘 이어주시면 됩니다.

유리함수의 역함수 공식 (+유도과정)
이번에는 유리함수의 역함수를 유도해보도록 할게요. 표준형, 기본형 둘 다 유도해볼 겁니다. 역함수 유도가 어려운 편은 아니지만 손이 많이 가니 시험 때는 공식을 외워서 쓰거나, 아니면 역함수 성질을 이용해서 바로 문제 푸는 걸 추천드려요. 매번 유도하는 건 시간이 모자라니까요-,
아, 그리고 유도는 보통 x로 식을 정리한 다음 문자를 바꾸는데, 저는 그냥 문자부터 바꾸고 정리했답니다. 이 편이 더 쉬운 것 같더라고요..!

표준형의 경우에는 대칭점인 (p,q)가 (q, p)로 바뀐다고 생각하시면 굳이 공식 안 외우셔도 되겠죠? k는 폭이니 대칭한다고 바뀌진 않을 테니까요.
이번에는 일반형을 살펴봅시다.

일반형의 경우에는 분모/분자에
동시에 -1을 곱한 꼴로도 나오기 때문에,
형태를 하나만 외우지 마시고,
부호 정도는 바뀔 수 있다-고
기억하시면 됩니다.

정리해볼까요?

뭐, 공식을 외우는 것도 중요하지만, 꽤 많은 문제가 직접 역함수 구하지 않아도 풀리는 경우가 많으니, 이 단원은 무조건 대입하기보단 유리함수 그래프의 특징을 잘 익혀서 풀도록 해요.
그럼 열공하세요!
'고등수학 (2015 개정 교육과정) > 고등수학(하)' 카테고리의 다른 글
| [경우의 수, 확률] 3의 배수 만들기 (3으로 나눈 나머지 이용) (2) | 2022.11.06 |
|---|---|
| 코시 슈바르츠 부등식 항 3개 이상 일 때 (등호 조건 및 증명) (0) | 2022.09.25 |
| 산술기하 평균 부등식의 모든 것 (연습용 문제 다수 수록) (2) | 2022.07.17 |
| 명제의 거짓 반례 조건 (0) | 2022.02.19 |
| 우함수, 기함수 곱/합성 성질 정리 (0) | 2021.11.13 |