오늘은 이차방정식에서 계수를 통해
근을 빨리 구하는 방법을 배워보도록 할게요.
원래는 근과 계수와의 관계를 이용하여
합과, 곱을 구하고 식을 직접 구성하면 됩니다.
그렇지만, 객관식인 경우에는
아래와 같이 바로 구할 수 있어요.

이차방정식의 근이 주어졌을 때,
역수이거나, 부호가 반대이면
계수를 통해 바로 방정식을 구할 수 있답니다.
물론 그냥 외워!!가 아니고,
왜 이런 관계식이 나오는지 설명도 해드릴게요.
그럼 살펴볼까요?
1. 역수를 근으로 갖는 이차방정식 구하기


순서를 거꾸로 써서 정리해볼까요?

괄호를 이용하여 표현해볼게요.

제곱형태를 정리해준다면 이렇게 되겠군요.

아니 이것은..!!

위와 같은 방법을 사용한다면
나머지 한 근도 증명할 수 있습니다.
즉, 계수의 순서를 반대로 쓴 방정식은,
원래 방정식 근의 역수를 근으로 갖습니다.

2. 부호가 다른 근을 갖는 이차방정식

시작은 위와 같습니다.

마이너스 x 마이너스 = 플러스이므로,
가운데 일차항을 변형해줍니다.
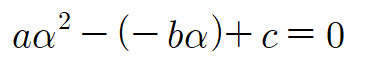
정리를 다시 해봅시다.
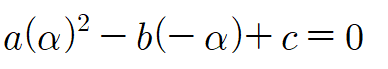
-a와 a는 모두 제곱하면 같아지므로, 변형해줍니다.

아니 이것은..!!

즉, 일차항 계수의 부호만 반대로 쓴 방정식은,
원래 방정식 근의 반대 부호를 근으로 갖습니다.

3. 역수에 부호가 반대라면?
위에서 배운 둘을 잘 섞어주시면 됩니다.
즉, 계수를 역방향으로 쓴 다음,
일차항 계수 부호를 바꿔주면 되죠.
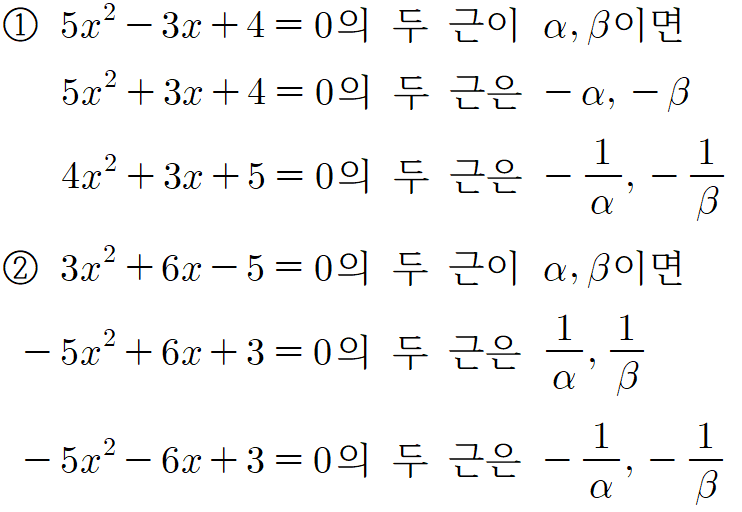
오늘 배운 내용을 일반화해서 기억하면 됩니다.

글보다 영상으로 보고 싶으신 분들은
사실 오늘 배운 내용은 이차방정식 뿐만 아니라,
삼,사차 그 이상의 고차방정식에서도 동일하게 성립합니다.
유도 과정은 동일하니,
아래 포스팅 참고하시면
도움이 될 거에요.
https://ladyang86.tistory.com/99
삼차방정식 - 역수를 근으로 갖는 방정식 외 기타
이전에 이차방정식을 배우면서 계수를 통해 근을 빨리 구하는 방법을 배웠던 것 기억 나시나요? 근이 역수거나, 음수인 경우에는 금방 구할 수 있었죠. 만약 기억이 안 나신다면 아래 포스팅을
ladyang86.tistory.com
그럼 다음에도 유용한 내용으로 돌아올게요!
'고등수학 (2015 개정 교육과정) > 고등수학(상)' 카테고리의 다른 글
| 정수조건 부정방정식의 해 (인수분해 형태로 바꾸기) (0) | 2020.11.21 |
|---|---|
| 세 점의 좌표로 삼각형의 넓이 구하는 공식 (사선공식, 신발끈공식) (3) | 2020.11.12 |
| [사차방정식 근의 성질] 복이차식 치환해서 근의 부호로 풀기 (0) | 2020.03.20 |
| [절댓값] 절댓값의 성질 (방정식, 부등식, 함수에 모두 사용됨) (0) | 2020.03.15 |
| [삼차방정식의 근] x^3=1의 허근 w의 성질 (0) | 2020.03.07 |