문자가 2개인데 식이 1개 뿐인 경우에는 해가 무수히 많이 나옵니다.
예를 들어 2x-y=0의 해는 (1,2), (2,4) ..., (10,20)... 등 무수히 많죠.
부정방정식이란?
일반적으로 문자의 개수보다 식의 개수가 더 적을 때는 위처럼 해가 무수히 많이 나옵니다. 이런 방정식을 부정방정식이라고 부릅니다.
부정이 한자로 아닐 부(不) + 정할 정(定)자를 써요. 해가 무수히 많이 나오기 때문에 하나로 정할 수 없는 방정식인 거죠. 그런데 이러한 부정방정식에도 특수한 조건이 붙으면 해를 유한개 구할 수 있습니다. 오늘은 그 중 '정수 조건'이 붙어 있는 부정방정식을 풀어볼 거에요.
강제로 인수분해하기
사실은 공통인수로 묶어서 더하고 빼준다는 개념인데, 상수를 제외하고 나머지 문자가 나오게끔 처음부터 항을 맞춰주시면 됩니다.
아래 예시를 보면서 따라해볼까요?
예제 1.
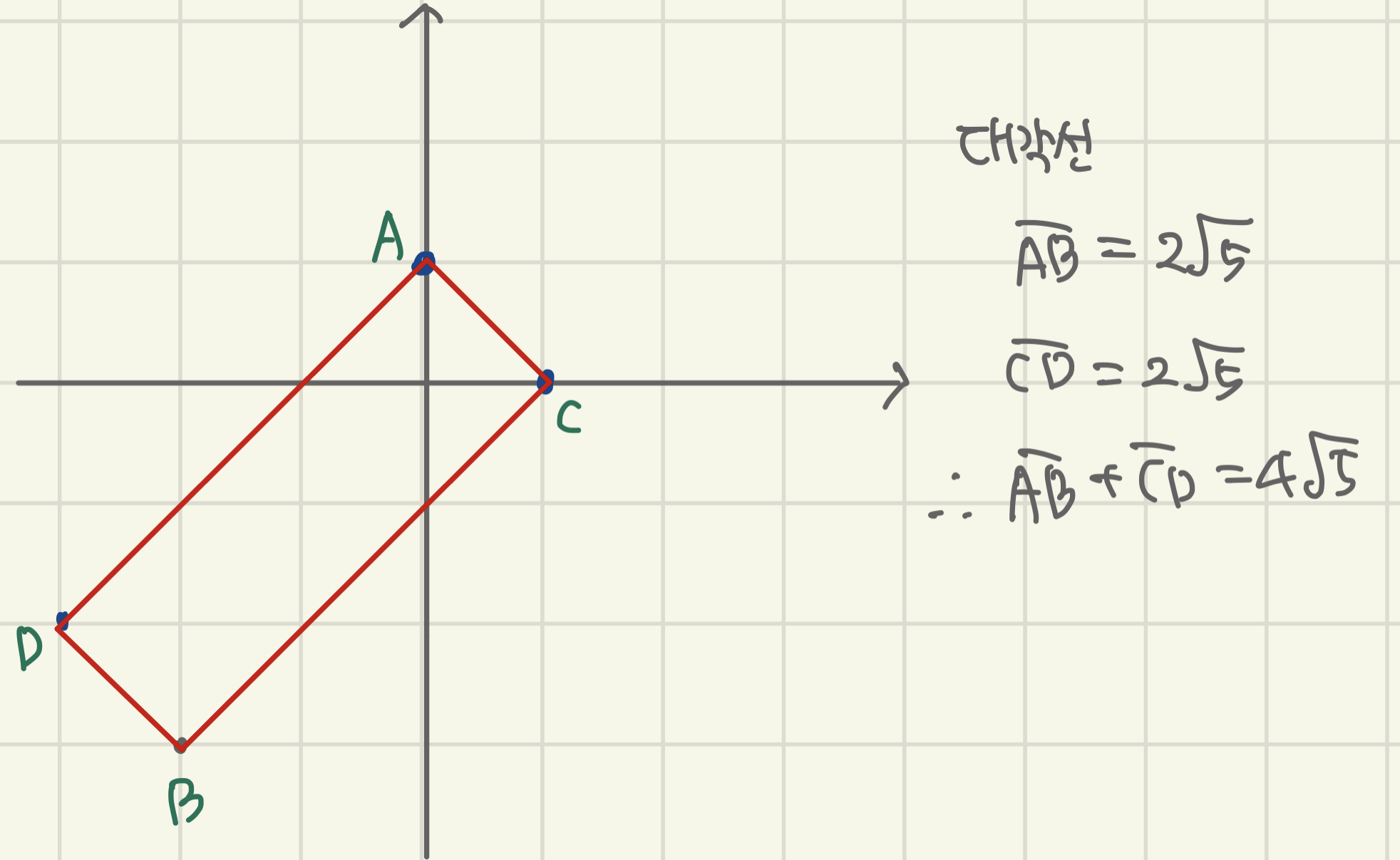
xy에 대한 방정식 xy+x+y-1=0을 만족하는 정수 x,y를 좌표평면 위의 점 (x,y)로 나타낼 때, 이 점들을 꼭짓점으로 하는 사각형의 두 대각선의 길이의 합을 구하여라.

이 때 xy+x+y를 만들기 위해 식을 (x+1)(y+1)로 인수분해 하려면 1이 더 필요함을 알 수 있죠. 그래서 맨 위의 식 양변에 1을 더해줍니다.

이제 곱해서 정수가 되는 수를 찾으면 됩니다. 부호를 고려해서 풀어주고, 실제 (x,y)의 순서쌍까지 다 구해주시면 됩니다.
위에서부터 순서대로 ABCD를 썼지만 실제로 그림을 그려보면 이 사각형은 ADBC가 되는군요. 반드시 그래프에 그려서 판단합시다 :-)
예제 2.

우선 이차방정식이 중근을 가지려면
판별식 = 0이어야 합니다.
일차항 계수가 짝수이므로 D/4=0를 씁시다.

부정방정식이므로 식을 변형해주면 됩니다.
다행히 13이 소수이므로 경우는 4가지만 나옵니다.

ab의 최댓값을 구하는 것이 목표이므로
모든 경우를 다 계산해보셔야 합니다.
부정방정식 형태를 인수분해하는 것만 좀 더 연습해볼까요?
예제3. xy+2x-y+1=0
(x-1)(y+2)=-3
예제4. xy+3x+2y+1=0
(x+2)(y+3)=5
핵심은 앞의 세가지 문자가 나올 수 있도록 맞춰주는 것입니다.!
이렇게 바로 될 때까지 열공하셔요^^
'고등수학 (2015 개정 교육과정) > 고등수학(상)' 카테고리의 다른 글
| 곱셈공식의 변형 - (문자가 2개인 경우, 거듭제곱) (0) | 2021.03.05 |
|---|---|
| 삼각형 무게중심 성질 (m:n 내분점의 무게중심, 거리 제곱의 합) (0) | 2021.02.13 |
| 세 점의 좌표로 삼각형의 넓이 구하는 공식 (사선공식, 신발끈공식) (3) | 2020.11.12 |
| [이차방정식 꿀팁] 역수를 근으로 갖는 방정식 빨리 구하는 방법 (0) | 2020.05.31 |
| [사차방정식 근의 성질] 복이차식 치환해서 근의 부호로 풀기 (0) | 2020.03.20 |