반응형
오늘은 수학적 귀납법에서 종종 등장하는
점화식 유형 하나를 다뤄볼까합니다.
원래는 치환해서 푸는 내용까지
교육과정에 있었는데요-,
삭제되었습니다.
다만, 교육과정에서 목표하는
'n에 차례로 수를 대입해서 구한다'는 방법으로
일반항을 제외한 특정항의 경우에는
값을 구할 수 있습니다.
그래서 (아직까지도)
몇몇 교재에서 다루거나,
알려주시는 선생님들이 계셔서
포스팅하게 되었습니다.
바로 등차수열도, 등비수열도 아닌-
마치 일차함수처럼(?) 생긴 점화식이죠.
(p가 1이면 등차수열이 되고,
q=0이면 등비수열이 되기 때문에
그냥 일반항을 바로 구할 수 있습니다.)

오늘은 이 수열에서
차례로 n에 숫자를 대입하는 방법 말고,
직접 일반항을 구하는 방법을
배워볼 예정입니다.
단계는 아래와 같습니다.
1. 우선 주어진 식을 등비수열의 형태로 만들어서 치환해줍니다.
2. 등비수열의 일반항을 구합니다.
3. 2.를 이용하여 원래 수열을 구합니다.

이를 이용하여 예제를 하나씩 풀어보도록 해요.!
문제1.
다음 주어진 수열의 일반항을 구하여라.
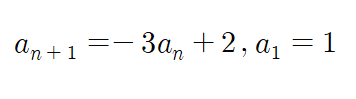

문제2
다음 주어진 수열의 일반항을 구하여라.


일반항을 구하는 게 교육과정도 아니고,
사실 꼭 위의 내용을
완벽하게 익힐 필요는 없습니다.
다만, 점화식으로 구해야 하는 항이
6,7번째만 되더라도 저 같은 경우에는
계산이 약해 대입이 너무 힘들어서..
점화식이나 수열 파트에서 종종 나오는
유형이므로 이왕이면
배워가는 편이 더 좋겠죠?ㅎㅎ
그럼 화이팅입니다!
반응형
'고등수학 (2015 개정 교육과정) > 수학1' 카테고리의 다른 글
| 지수/로그 방정식 치환해서 푸는 유형 (0) | 2022.04.01 |
|---|---|
| 거듭제곱근 정의 관련 문제 모음 (0) | 2022.03.30 |
| 시그마 기호의 성질 정리 (증명과 주의점) (0) | 2022.01.22 |
| 지수함수와 로그함수의 평행이동, 대칭이동 주의사항 (0) | 2022.01.14 |
| 5종 교과서 수학적 귀납법 문제 모음 (2015 개정기준) (1) | 2021.06.13 |