거듭제곱근 중 실수의 개수에 관한
문제들을 풀어볼 거예요.
개념 정리가 머릿속에 딱! 되어있으면
굉장히 쉽게 풀 수 있습니다.

우선
거듭제곱근의 정의는 아래와 같습니다.

보통 근호를 이용해서 표현하는데,
옳지 않은 표현이니 습관 들이지 마세요!

n제곱근은 n개 존재합니다.
복소수 범위에서는요.
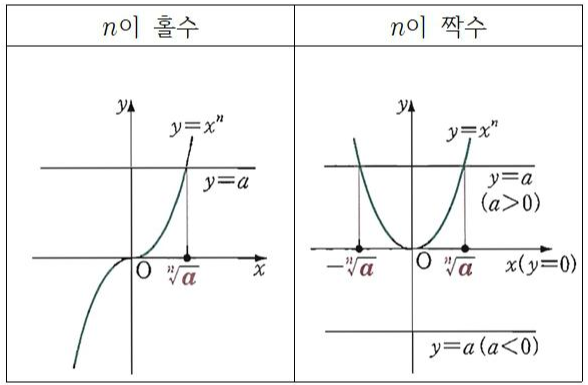
실수 범위에서는
아래와 같이 그래프를 그려서
위치를 판별할 수 있습니다.
그런데 문제는 a 대신
x라는 변수를 더 많이 씁니다.
위에서 정의로 배운 a의 거듭제곱근보다
x의 n제곱근이라는 표현이
더 자주 나오죠.

여전히 실수의 개수는 그래프로
보시면 됩니다.
여기서 포인트는 n이 홀수냐/짝수냐
x가 양수냐 음수냐가 되겠죠?

크게는 n제곱근이라 하면
n이 홀수인지/아닌지부터 판별합시다.
홀수면 무조건 1개니까요.
짝수면 부호를 판별해서
2/1/0 중 하나가 되겠죠?
이제부터 실제로 문제를 풀면서
차근히 익혀보도록 해요!
문제 1

헷갈리니까 x와 n을 표시를 먼저 해둘게요.

n이 홀수인 경우에는 항상 1개고,
짝수인 경우에는 부호를 보시면 되겠죠?

문제 2

n제곱근이라고 나와있네요.
역시나 문제에서 준 n과 x가 뭔지
먼저 파악한 다음,
n의 홀짝-> x의 부호 순으로
살펴봅시다.

문제 3
출처 : 2022년 수능특강 수학 1 Ch1. Lv2 #1

이제 이쯤 되면 눈으로 풀립니다.
역시나 n이 홀수인 3과 5인 경우는 1이죠.
4와 6의 경우에는
b와 ab의 부호를 보고 판단합니다.
b <0이고, a <0이니 ab>0
f4(b)=0이고
f6(ab)=2가 됩니다.
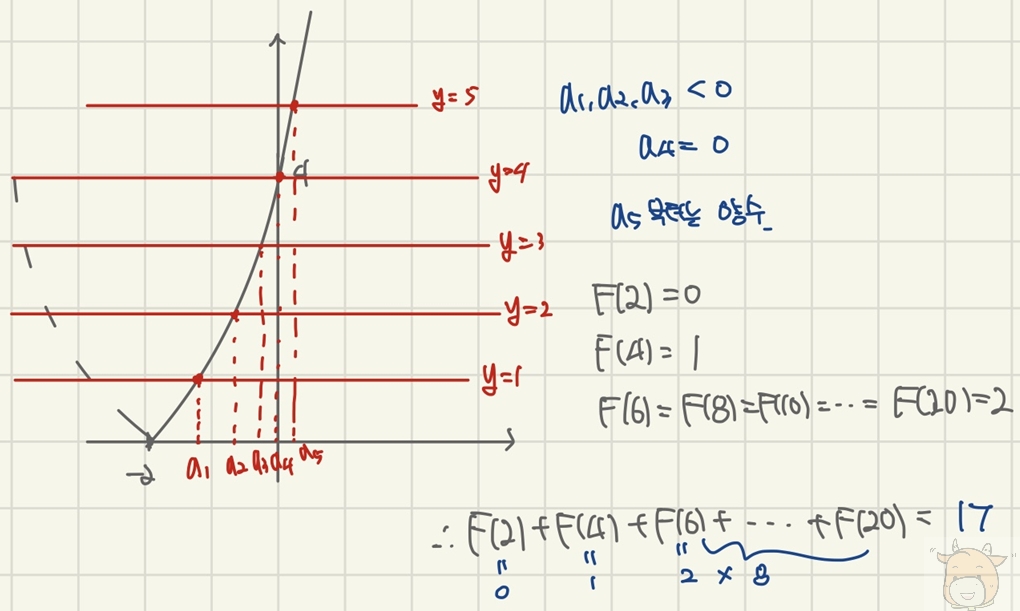
문제 4

n제곱근이니 먼저 n의 홀짝으로 판단하고,
이후에는 an의 부호를 보시면 됩니다.

홀수일 때는 항상 1이므로,
그냥 홀수가 몇 개 나오는지만
잘 세어주시면 됩니다.

여기서는 an의 부호를 알기 위해
직접 구해보도록 할게요.
부호를 보는 게 포인트니
그래프로 대략적인 개형만 보셔도
충분합니다.
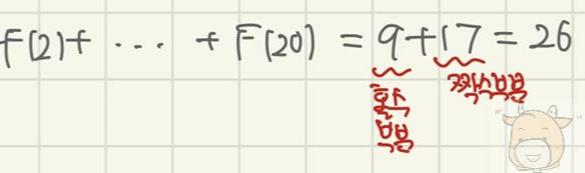
(240511 추가함)
문제5
2024년 5월 고3 모의고사 #19
집합 U={ x | -5 ≤ x ≤ 5, x는 정수}의 공집합이 아닌 부분집합 X에 대하여 두 집합 A, B를
A= { a | a는 x의 실수인 네제곱근, x∈X }
B= { b | b는 x의 실수인 세제곱근, x∈X }라 하자.
n(A)=9, n(B)=7이 되도록 하는 집합 X의 모든 원소의 합의 최댓값을 구하시오.
정답 : 11
원소 7개인데, 음수 2개, 0, 양수 4개로 구성하면 된다. 최댓값이 되어야 하므로, X= {-2, -1, 0, 2, 3, 4, 5}
위 문제가 잘 풀린다면
내신 대비용으로 아래 포스팅을
참고하시는 것도 도움이 될 거예요.
[지수] 거듭제곱근 실근의 개수 (내신 선별)
실근의 개수 오늘은 거듭제곱근 중 실근의 개수에 대한 내용을 정리하고 문제를 풀어보겠습니다. 이건 중요한 내용이라 이전에도 포스팅을 했었습니다. 그래서 간단한 기본기 문제를 풀고 싶으
ladyang86.tistory.com
항상 수학은 정확한 개념 정리가
가장 중요합니다!
그럼 열심히 공부하고 다음에 봐요^^
'고등수학 (2015 개정 교육과정) > 수학1' 카테고리의 다른 글
| 지수함수와 로그함수의 평행이동, 대칭이동 주의사항 (0) | 2022.01.14 |
|---|---|
| 5종 교과서 수학적 귀납법 문제 모음 (2015 개정기준) (1) | 2021.06.13 |
| 지수, 로그 - 두 가지 방법으로 푸는 문제 (0) | 2021.03.20 |
| 지수/로그함수 그래프로 대소비교(ㄱㄴㄷ문제) (0) | 2020.11.07 |
| [삼각함수의 활용] 삼각형의 넓이 공식 5가지 (0) | 2020.10.04 |