삼각함수의 활용에서는 삼각형의 넓이를 자주 구합니다.
삼각형의 넓이를 구하는 공식 5가지를 살펴볼거에요. 꼭 외워주세요!

5가지를 그냥 다 외우려면 상당히 복잡하므로, 우선 크게 1,2,3을 묶어서 같이 외우고 4,5를 외울게요.
①②③은 사인법칙으로부터 파생되는 것
④ 헤론의 공식
⑤ 내접원의 반지름과 둘레의 길이로 구하는 방법입니다.
하나씩 차근히 살펴보도록 해요.

가장 기본적인 공식이죠. 중3 때부터 외운 것일 테니 넘어갈게요!
여기에 사인법칙을 잠깐 기억해볼까요?

식에서 sinC를 사인법칙을 이용하여 바꿔주기만 한 것인데 ② 공식이 나왔군요.!
사인법칙 한 번 더 써볼까요?
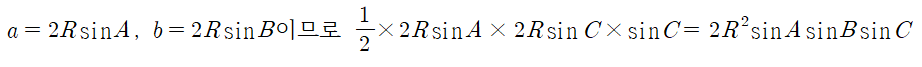
이번에는 두 변 a,b를 사인법칙을 이용하여 바꿔주었더니 ③ 공식이 같이 나왔어요.
①만 알면 ②,③은 사인법칙으로부터 유도할 수 있으니 한 큐에 외웁시다!
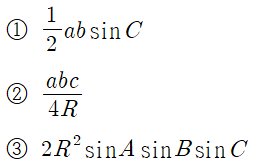
외우셨나요?
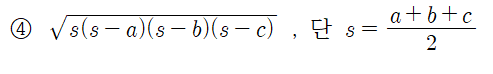
헤론의 공식이라고 불리는 4번째 공식입니다. 세 변의 길이의 합이 짝수라면 굉장히 간단하게 연산이 되죠. 물론 아닐 때도 얼마든지 사용 가능합니다 :-) 넓이를 구하는데 있어 각을 몰라도 되기 때문에 손쉽게 구할 수 있죠.
유도과정이 궁금하시다면 아래 포스팅을 참조하시면 됩니다.
https://ladyang86.tistory.com/113
헤론의 공식 증명 (세 변의 길이로 넓이 구하는 방법)
오늘은 삼각형의 세 번의 길이를 알 때 넓이를 바로 구할 수 있는 공식을 알아볼 거에요. 여러분, 이렇게 세 변의 길이가 주어진 삼각형의 넓이를 어떻게 구하시나요? 당연히 높이가 필요하니까
ladyang86.tistory.com

중학교 2학년 때 내심을 배우면서 익히는 공식이죠. 이것도 증명은 중등 과정이니 생략하도록 할게요!

외접원의 반지름 R, 내접원의 반지름 r, 그리고 변의 길이, 각 등 다양하게 들어있죠?
그래서 다 외우고 나면, 상황에 맞게 필요한 공식을 바로 적용할 수 있어요.
그리고 만약 길이나 각에 대한 정보가 아니라, 좌표가 주어진 거라면 신발끈 공식을 사용하시면 됩니다.!
https://ladyang86.tistory.com/60
세 점의 좌표로 삼각형의 넓이 구하는 공식 (사선공식, 신발끈공식)
학교에서는 안 알려주지만 학원에선 반드시 알려주는 공식들이 있죠. 오늘 다뤄볼 내용은 그 중 하나인 신발끈 공식입니다. 삼각형의 넓이를 구할 때, 세 점의 좌표로 바로 구할 수 있는 방법이
ladyang86.tistory.com
그럼 힘내서 외워두도록 해요.^^
'고등수학 (2015 개정 교육과정) > 수학1' 카테고리의 다른 글
| 지수, 로그 - 두 가지 방법으로 푸는 문제 (0) | 2021.03.20 |
|---|---|
| 지수/로그함수 그래프로 대소비교(ㄱㄴㄷ문제) (0) | 2020.11.07 |
| [수열] 등차수열의 합으로부터 등차수열의 일반항 빨리 구하는 방법 (0) | 2020.06.28 |
| [등차수열] 등차수열의 일반항 쉽고 빠르게 구하는 방법 (0) | 2020.03.16 |
| [지수함수/로그함수] 고난도 역함수 구하는 문제 (0) | 2020.02.21 |