나는 문과라 도저히 미적분이랑 뭘 엮어야 할지 모르겠다고 고민되는 분이라면 오늘 포스팅 집중!
사회계열, 철학계열까지 충분히 커버가능한 주제를 갖고 왔답니다.
바로 접선에 개념 변화를 정반합의 과정과 엮어서 살펴볼까 합니다.

문과를 위한 수학탐구 추천주제
우선 라카토스의 수학관은 아래와 같습니다.
수학은 추측 - 증명 - 반박의 끊임없는 개선을 통해 성장하는 '준경험주의적 과학'이라는 것이죠.
라카토스의 지식의 성장 과정은 아래와 같습니다.
1) 수학적 추측 제기
2) 원래 추측을 부분추측으로 분해
3) 반례의 등장 & 추측과 증명을 반박
4) 추측과 증명을 개선
(이 부분은 좀 더 자세히 쓰자면 교육학 쪽에서 다루어야 하니 일단은 지양하죠.)
헤겔의 변증법, 라카토스의 수학관 등 인문학쪽에서도 엮을만한 소재가 꽤 많죠.
아무튼 수학2에서 배운 접선의 개념을 통해, 이전까지 살펴보았던 접선의 개념들을 살펴보며 이 개념이 어떻게 변화해왔는지를 관찰해보고자 합니다.
인식론적 장애
: 어떤 특정한 맥락에서 성공적이고 유용하였던 지식이 인지 구조의 일부가 되었지만, 새로운 문제 상황이나 더 넓어진 문맥에서는 부적합해진 경우.
우리는 인식론적 장애로 접선을 살펴볼거랍니다.
즉, 접선과 같이 인지적 갈등을 일으키는 개념에 대해
반례가 출현함으로써,
기존의 추측이나 정의, 증명이 새롭게 수정되어 가는 과정을 보려는 것이죠.
학교 수학에서 어떤 개념을 도입할 때에는 그 개념에 대한 모든 맥락을 제시하지 못할 수도 있습니다.
우리가 포물선에 접선 그으면서 '평균 변화율의 극한' 이렇게 지도할 수는 없잖아요..?
그래서 불가피하게 (혹은 의도적으로) 제한된 맥락 속에서 개념을 도입하게 됩니다.
그러다보면 이는 완전하지 않아서 나중에 반례가 등장하게 되면 기존 지식과 부딪혀 수정하게 되죠. 아래 예시를 통해 같이 살펴보도록 해요.
중학교 1학년 : 원과 직선의 위치관계를 배울 때 접선을 처음 배웁니다.
이 때 접선은 '원과 한 점에서 만나는 직선'으로 정의하죠.

이 정의는 중3 때 포물선에 접선 그을 때 반례가 나옵니다.
아래와 같이 y축과 평행한 직선은 포물선과 한 점에서 만나지만 접선이 아니거든요.
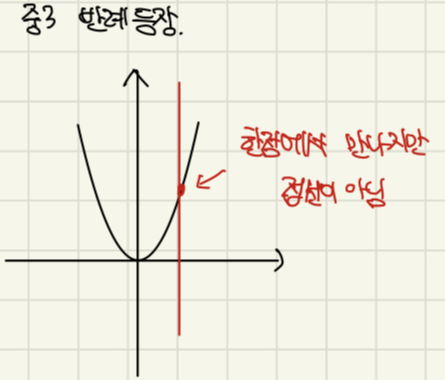
그래서 아래와 같이 접선을 '곡선과 스치면서 한 점에서 만나는 직선'으로 접선의 개념을 수정하게 됩니다.

이 정의는 판별식을 사용하여 구하면서 고1 내내 사용됩니다. 그러다가 고2 때 다른 함수들에 접선을 그으면서 당황하게 되죠. 아래 반례들을 살펴볼게요.
반례 1 : 한 점에서 스치면서 만나지만 접선 아님
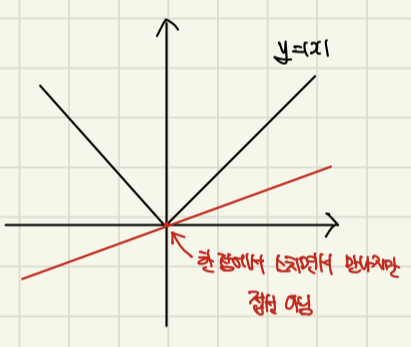
반례 2 : 관통하면서 한 점에서 만나지만 접선임

반례 3 : 두 점에서 만나지만 접선임.
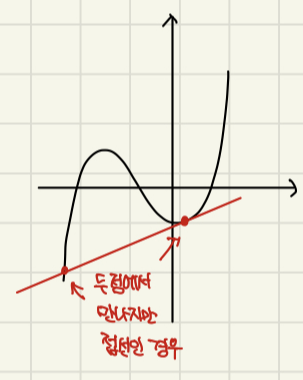
다양한 반례의 등장으로 접선에 대한 개념을 수정하게 됩니다.
마침 수학2에서 미분을 배우죠. 즉 '곡선 위의 한 점을 지나며 기울기가 그 점에서의 미분계수와 같은 직선'으로 정의합니다. 이 경우 관통하거나 두 점에서 만나도 상관없죠. 그리고 스치면서 지난다는 표현도 훨씬 정교하게 정의하게 됩니다.
그런데 생각해봅시다. 미분계수가 없으면 접선을 못 그을까요?

특히나 이렇게 뾰족한 함수는 미분이 불가능하기 때문에, 미분계수를 구할 수 없죠.

그렇지만 이 역시나 위의 원처럼
y축(x=0)이 접선으로 보이지는 않나요?
결국 우리는 할선의 극한으로 다시 접선을 정의할 수 있습니다.
미분계수가 존재하지 않지만
할선의 극한으로는 아래와 같이 정의가 가능하죠.

아래와 같이 원의 경우에도 x=2가 접선인데,
이 역시 할선의 극한으로는 정의 가능합니다.
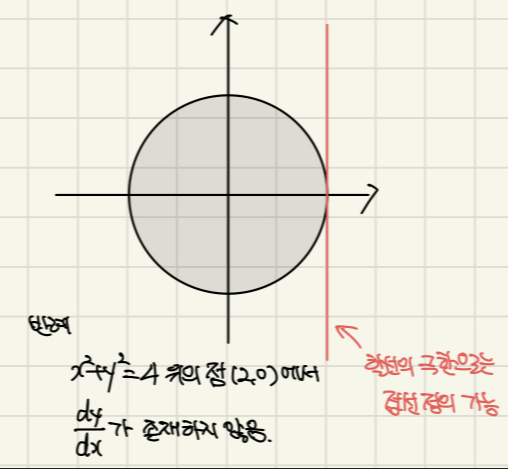
이런 개념을 정립하는 과정에서,
미분 가능하면 접선이 존재하지만,
역은 성립하지 않는다는 것도
다양한 반례를 통해 알 수 있죠.

정리해볼까요?
우리는 접선을 통해 반례를 통한 기존 지식의 수정이 어떻게 일어나는 지를 살펴보았습니다.
원래 있던 기존 지식에 반하는 예시가 등장함으로써, 이를 받아들이면서 점점 나아가는 모습이죠.
다음번에는 이렇게 살펴본 접선의 개념 변화를 교사는 어떻게 지도하면 좋을지도 한 번 써보도록 하겠습니다. 다음 포스팅은 교육 계열을 지망하는 학생들에게 좋은 아이디어가 될 것 같네요.
그럼 다음에도 유익한 포스팅으로 돌아오겠습니다!
'수학 for 학생 > 수학 주제연구 & 수학사' 카테고리의 다른 글
| 표본표준편차 - 표본분산을 n-1로 나누는 이유 (0) | 2023.06.04 |
|---|---|
| 수학1 수열의 합 공식 - 도형, 조합으로 증명 (0) | 2022.10.23 |
| 수학계의 베토벤, 레온하르트 오일러 : 논문을 가장 많이 쓴 수학자 (0) | 2020.08.26 |
| 미적분학을 배우는 이유 (feat. 미분, 적분의 유용성) (0) | 2020.04.26 |
| [수학사] 적분이 먼저 발견되었는데 미분부터 배우는 이유는? (0) | 2020.04.23 |