중2때 정오각형의 일부분을 떼서
닮음인 걸 배우죠.
중3때 황금비 배우는 것과
연결시킬 수 있습니다.
오늘은 그 부분을 총정리 해볼까 해요.
황금비의 정의
길이 a+b인 선분을
길이가 a,b인 두 선분으로 나누었을 때,
선분의 길이비가
전체 : 긴변 = 긴변 : 짧은변
즉, (a+b):a = a:b를 만족하면
이 선분은 황금비 Φ=a/b로
분할되었다고 하고,
이 분할을 황금분할이라고 합니다.
그러니까 그림으로 그려서 살펴보자면,
전체 : 긴변 = 긴변 : 짧은변 (우측)
여기서 길이 비를 말하는 것이므로
b를 1로 두고 식을 세울수도 있죠. (좌측)


자 다시 정리해볼게요.
선분의 길이비가
전체 : 긴변 = 긴변 : 짧은변이면

이제부터 정오각형을 살펴보죠!

정오각형의 한 변 길이와
대각선 길이는 황금비를 이룹니다.
지금부터 증명해봐요!
말고도 정오각형 모양 자체가
문제로 나오는 경우도 있으니,
증명을 꼼꼼하게 보도록 해요.
일단 정오각형이므로
모든 각과 변의 길이가 같습니다.
① 각 : ∠A=∠B=∠C=∠D=∠E=108 ˚
변 : AB=BC=CD=DE=EA
△ABE는 꼭지각이 108 ˚
이등변 삼각형입니다.


② 정오각형이므로 △ABE≡△BCA
모두 밑각이 36˚이므로
△FAB 역시 꼭지각이 108 ˚인
이등변 삼각형입니다.


③ 같은 방식으로 △FBA와 △JAE의 각을
모두 표기하면,
꼭지각이 36˚인 이등변 삼각형
△AFJ, △BCH, △ACD를
찾을 수 있습니다.
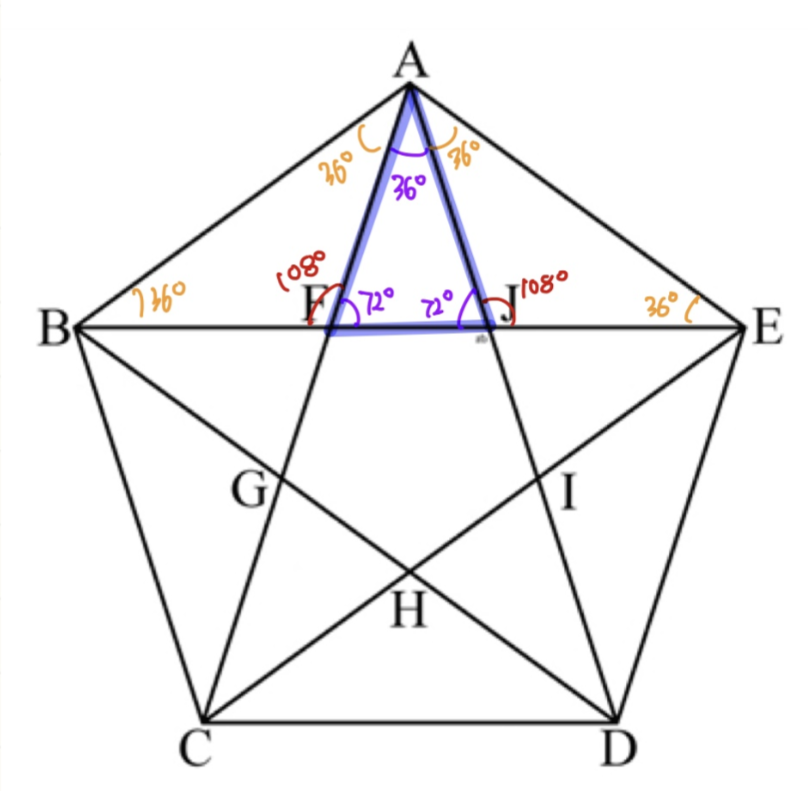

정리!
정오각형 모양에서는 아래와 같이
이등변 삼각형 2개가 보이셔야 합니다.


그래서 이 두 닮음 삼각형을 이용하여
비례식을 세우는 게 핵심이죠.


둘을 합친다면 아래와 같이 나옵니다.

가볍게 문제를 풀어봅시다.
예제1
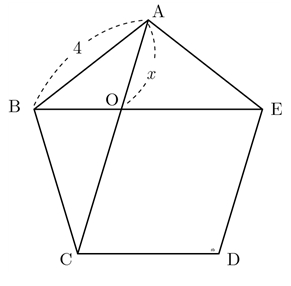
x의 값을 구해봅시다.

유사 황금비 (A4용지 길이비)
황금비는 아니지만
가로/세로 길이비가 일정하게 유지되는
도형들이 있습니다.
우리가 자주 사용하는 A4 종이 용지가 그렇죠.
가로/세로 길이비는
반으로 접어도 항상 같습니다.
식을 세운 다음
두 변의 길이비를 비교하면,
아래와 같이 간단하게 나옵니다 :-)
어차피 비를 구하는 것이니
한 변의 길이를 1로 두고 풀면 됩니다.

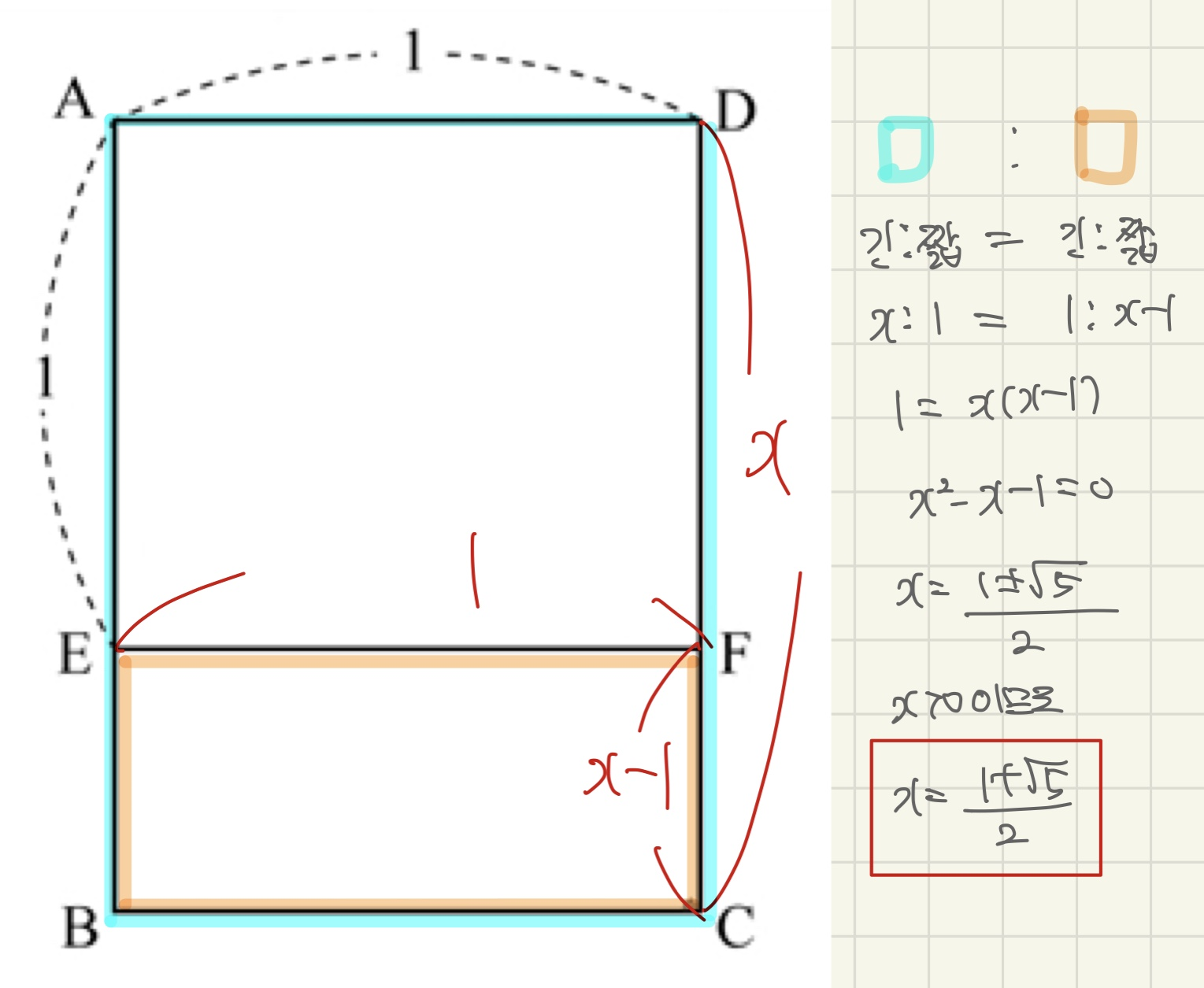
예제2
다음 그림의 두 직사각형 ABCD와 FEBC는
서로 닮음이다.
AD=AE=1일 때, DC의 길이를 구하시오.

두 개의 직사각형의 길이를 설정 후,
비례식으로 풀면 됩니다.
'중등수학 > 중등 3학년' 카테고리의 다른 글
| 헤론의 공식 증명 (세 변의 길이로 넓이 구하는 방법) (0) | 2021.08.26 |
|---|---|
| 루트와 제곱을 절댓값으로 바꾸는 방법 총정리 (0) | 2021.08.20 |
| 이차함수 부호에 따른 그래프 개형 총정리 (0) | 2021.06.29 |
| 순환소수, 무리수, 유리수 개념 정리 + ox 문제 (0) | 2021.04.22 |
| 곱셈공식의 변형 연습용 문제 모음 (0) | 2021.03.04 |