오늘은 기말고사 시험 대비로,
그래프 개형에 따른
이차함수 부호를 정리해볼까 합니다.

1. 일반형에서 a,b,c 정하는 법
아래와 같은 이차함수의 일반형에서

각 계수 a,b,c의 의미를 알아봅시다.
① a : 위/아래로 볼록을 결정

② b : 축의 위치를 결정

그냥 왼쪽부터 '같다'라고
외우시면 됩니다.

③ c : y 절편을 결정
y축과의 교점의 y좌표를 보고
결정하시면 됩니다.
x축 위에 있으면 0
x축 아래에 있으면 음수
x축 위에 있으면 양수죠
그럼 문제를 한 번 풀어볼까요?
문제1
아래와 같은 이차함수에서

a,b,c의 부호를 구하여라.


문제2
아래와 같은 이차함수에서

a,b,c의 부호를 구하여라.


2. 표준형에서 a, p, q 정하는 방법
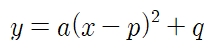
이 경우는 간단하게
꼭짓점의 부호를 보면 됩니다.
바로 문제를 풀어보죠!
문제3
아래와 같은 이차함수에서
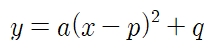
a, p, q의 부호를 구하시오.

풀이
a는 위/아래로 볼록으로 판단하고
꼭짓점의 x,y 좌표로 p,q를 판단합니다.

3. 그외 기타 고급 방법
위의 두 가지 방법은
이차함수 공부를 성실히 하셨다면
쉽게 풀 수 있죠.
지금부터 언급할 건,
고등 선행을 한 친구들은 쉽게해도
그냥 중3 과정만 한 친구들은
잘 못하는 내용이에요.
① 판별식
이차함수와 축과의 위치관계에 따라
근의 개수가 달라지죠.
근이 2개면 판별식 부호는 D>0
근이 1개면 판별식 부호는 D=0
근이 0개면 판별식 부호는 D<0
이걸 이차함수 그래프와
x축과의 교점의 개수로 같이
연결해서 보시면 됩니다.

② 함숫값
이 부분 설명하기 전에
잠깐 문제 하나 풀어볼까요?

①②③은 위에서 배운대로
a,b,c의 부호를 구해서 판단하시면 됩니다.
(a>0, b<0, c<0죠)
그런데 ④을 봤을 때,
양수가 2개(a, -b), 음수가 1개(c)니
합이 양수일까, 음수일까?
이런 고민 혹시 하시나요?
이런 경우에 +- 개수를 세면서
추측을 하시면 안됩니다.
(사실 아마 본인도 하면서 알긴 알거에요.
그러면 안된다는 것을..)
그럼 이럴 땐 어떻게 해야 할까요?
다시 주어진 함수를 살펴봅시다.

함수의 계수를 잘 살펴봅시다.
우리가 원하는 값을 어떻게 얻을 수 있을까요?

우리가 구하는 값은 위의 함수의 x의 값에다
x=-1, x=2를 차례로 대입한 값입니다.
그럼 이제 그래프에서 f(-1), f(2)의 부호를
찾아보시면 되겠죠?

그래프로 판단하면
④는 틀리고 ⑤는 맞습니다.
옳은 걸 구하는 문제니 답은 ⑤이죠.
그래프 개형으로 이차함수의 부호를 판단하는 문제는
시험에 꼭 등장하는 문제입니다.
부지런히 연습하셔서 꼭 다 맞길 바랄게요.
참,
일차함수의 그래프를 준 다음,
이를 이용하여 물어보는 경우도 있으므로
일차함수가 기억이 안난다면
그래프를 보고 기울기와 y절편의 부호 정도는
판단할 수 있도록 복습하고 가세요!
그럼 다음에도 유용한 포스팅으로 돌아올게요^^
'중등수학 > 중등 3학년' 카테고리의 다른 글
| 루트와 제곱을 절댓값으로 바꾸는 방법 총정리 (0) | 2021.08.20 |
|---|---|
| [이차방정식 활용] 정오각형과 황금비 (황금삼각형, 사각형) (2) | 2021.07.09 |
| 순환소수, 무리수, 유리수 개념 정리 + ox 문제 (0) | 2021.04.22 |
| 곱셈공식의 변형 연습용 문제 모음 (0) | 2021.03.04 |
| 삼각비 특수각이 아닐 때 객관식 문제 (0) | 2020.11.20 |