정적분 넓이 공식 (이차함수 근, 삼차함수 중근)
오늘은 굉장히 자주 사용되지만, 증명하기에 너무 오래 걸리기 때문에 반드시 외워야하는 적분 넓이 공식 두 가지를 살펴보려고 합니다.
첫번째는 가장 일반적으로 쓰이는 이차함수 넓이공식입니다.
1. 이차함수의 넓이 공식

이차함수와 축, 이차함수와 직선,
두 이차함수로 둘러싸인 부분의 넓이도
동일하게 구하시면 됩니다.

증명은 아래와 같이 직접 하시면 됩니다.
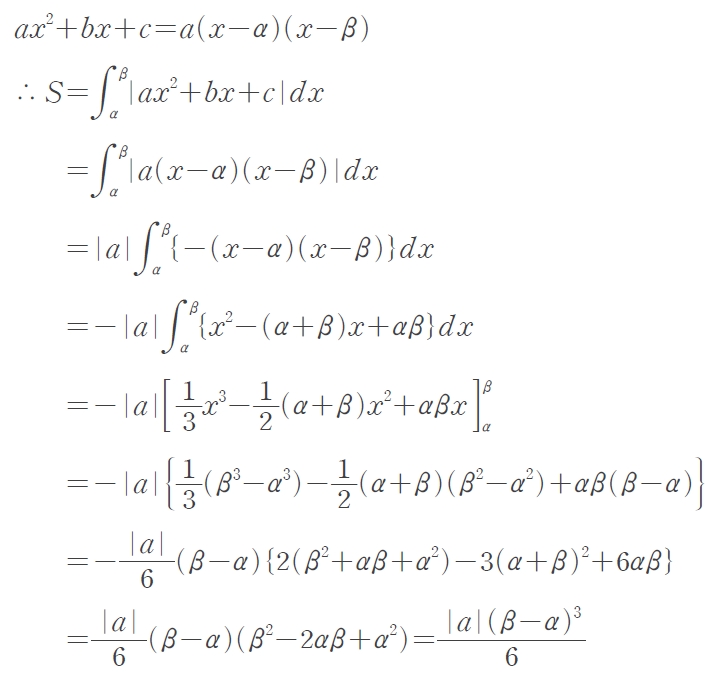
음.. 보면 아시겠지만, 이걸 매번 직접 계산한다면 매우 힘들겠죠? 게다가 두 근이 정수가 아니라 분수나 무리수가 나온다면 더 계산이 복잡해질테니, 되도록이면 공식을 외워서 쓰도록 합시다. 이건 대상이 최고차가 이차인 다항함수 사이에서는 항상 쓸 수 있는 방법이에요.
그럼 예시 문제를 몇 개 풀어볼까요?
예제1


예제2


예제3


여기서 중요한 것!
최고차항의 계수 함부로 없애면 안됩니다.
2. 삼차함수와 접선으로 둘러싸인 넓이
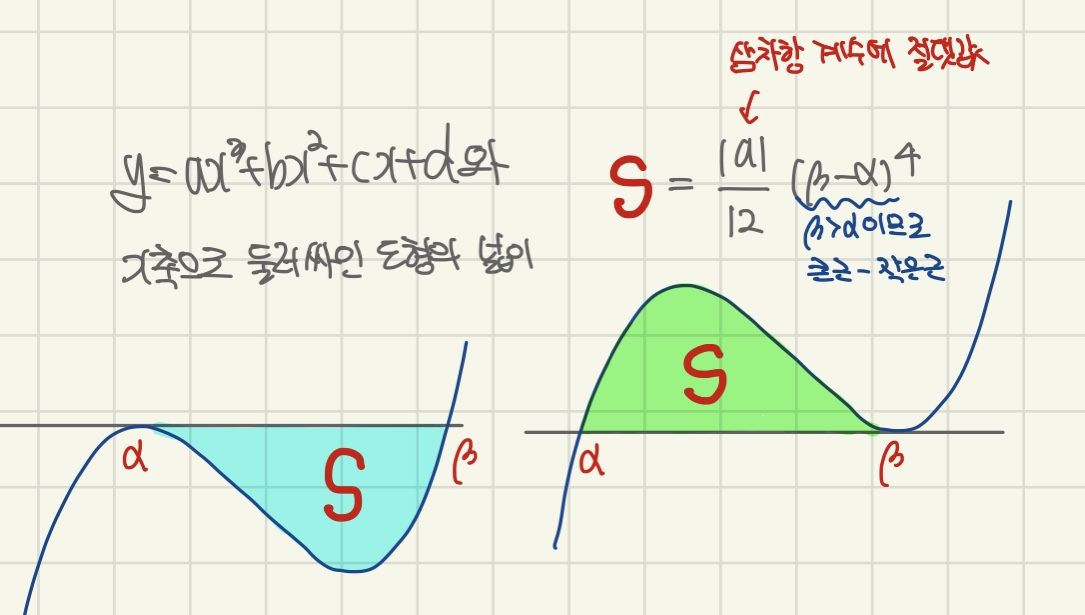
이것도 마찬가지로 등장 빈도가 높은 편이라 그냥 외우시는 게 편합니다. 굳이 외워야하냐?고 물어보신다면, 역시나 아래와 같이 유도하는 것이 너무나 버겁기 때문이죠. 아래는 삼차함수와 접선으로 둘러싸인 부분의 넓이를 유도 해보았습니다.

그럼 이것도 마찬가지로 문제를 여러개 풀어서 익혀보도록 해요!
예제4

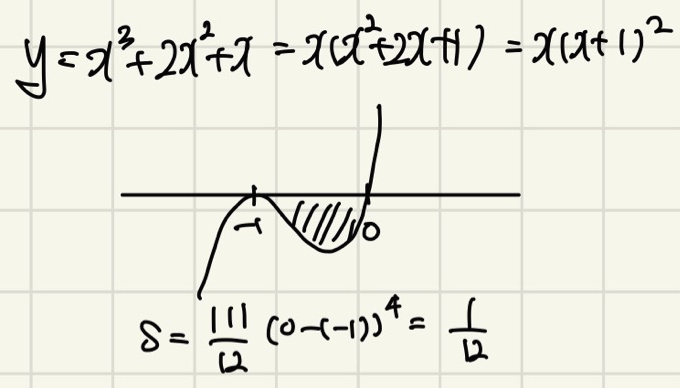
예제5


예제6

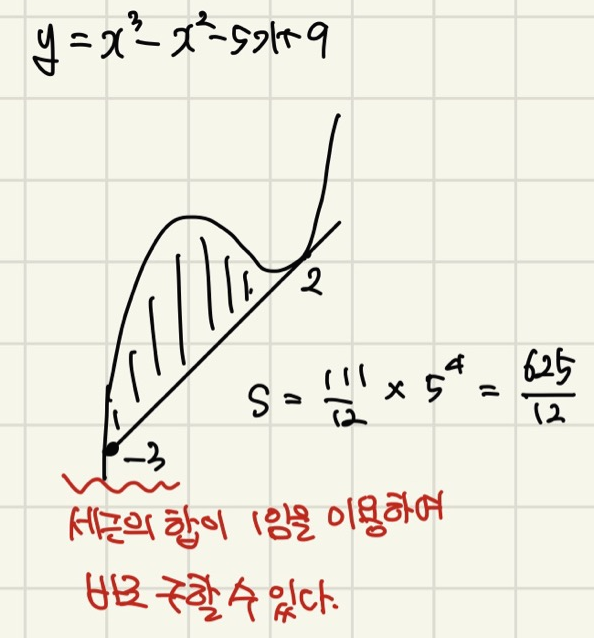
적분 자체가 계산이 오래 걸리는 데다가 접선까지 구해서 연립하려면 정말.. 시험 시간에는 많이 힘들죠. 그러니 특히나 미분과 적분에 대한 여러 팁들은 꼭 익히도록 해요!
아, 그리고 사실은 사차함수의 경우에도 접선으로 둘러싸인 부분의 넓이를 구하는 공식이 있습니다...만 이건 자주 등장하는 건 아니라.. 공식을 외울 필요까지는 없을 것 같아요.! 혹시나 다룰 일이 있다면 나중에 또 포스팅 하겠습니다.
해당 포스팅 내용 그대로 유튜브에도 간단하게 10분 정도 되는 강의 업로드 하였으니 같이 보시면 도움이 되실 거에요.^^
수학2 필수 암기 공식 - 정적분의 넓이 공식 (이차함수, 삼차함수 접선) - YouTube
'고등수학 (2015 개정 교육과정) > 수학2' 카테고리의 다른 글
| 삼차함수 위의 한 점에서 그은 접선이 곡선과 다시 만나는 점 (0) | 2022.02.25 |
|---|---|
| f(x+y)=f(x)+f(y)+p(x) 꼴 정리 (관계식이 주어진 경우의 미분,적분) (2) | 2022.02.12 |
| 함수의 연속 진위 판정 (합성함수 포함) (1) | 2021.10.17 |
| 합성함수의 미분법 (다항함수의 거듭제곱) (0) | 2021.09.23 |
| 사차함수 중근의 성질 - 2011년 7월 나형 20번 해설 (0) | 2021.09.11 |