오늘은 함수의 수렴과 연속의 성질들을 쉽게 외우는 방법에 대해 알아보겠습니다.
우리가 고2 내신을 준비하다보면, 진위 판정을 한 번쯤은 해보게 됩니다.
이게 은근 어렵죠.
나중에 좀 더 쓸텐데 진위판정에서는
되는 성질을 잘 외우시는 것이 중요합니다.
먼저 가장 기본적인 성질들을 살펴보기 전,
간단한 개념 하나만 살펴봅시다.
이항연산에서 '닫혀있다'라는 개념입니다.
A라는 집합과 *라는 연산에 대하여
연산 결과가 항상 A라는 집합에 포함된다면,
A는 *에 대하여 닫혀있다고 표현합니다.
영어로는 말 그대로 Close
예시를 들자면,
자연수 집합 N과 덧셈 연산+을 살펴보면,
자연수 + 자연수 = 자연수가 되죠.
이 때 +는 N에 대하여 닫혀있다고 표현합니다.
그럼 뺄셈은 어떨까요?
자연수 - 자연수 = 항상 자연수가 되나요?
아니죠. 3-5=-2인데 -2는 자연수가 아닙니다.
그래서 -는 N에 대하여 닫혀있지 않다고 표현합니다.
혹은 열려있다고 표현도 있긴 합니다만,
거의 사용되는 걸 못 본 듯 해요.
그러니까 이 닫혀있다는 표현은
어떤 집합이냐, 어떤 연산이냐에 따라
다 달라지는 거죠.
자연수는 덧셈과 곱셈에 대해서는 닫혀있지만,
뺄셈과 나눗셈에 대해서는 닫혀있지 않습니다.
그럼 이제 다른 연산들을 살펴봅시다.
우리가 아는 집합 중 유리수와
간단한 사칙연산을 살펴봅시다.
유리수의 사칙연산
유리수끼리는 더해도, 빼도 유리수입니다.
유리수 + 유리수 = 유리수
유리수 - 유리수 = 유리수
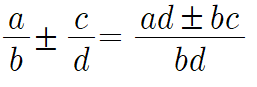
유리수끼리는 곱셈과 나눗셈을 해도 유리수죠.
유리수 x 유리수 = 유리수
유리수 / 유리수 = 유리수


즉 사칙연산에 대해서
유리수와 유리수를 연산하면
결과가 항상 유리수가 나옵니다.
즉, 유리수는 모든 사칙연산에 대하여
닫혀있네요.
사실 이런 수집합은 인류 역사상
유리수가 처음이었습니다.
모든 사칙연산에 대해서 닫혀있다니,
유리수는 완벽한 수야!!
-라고 옛날 사람들은 생각했다네요.
그래서 당시 사람들은
유리수가 아닌 수가 등장했을 때,
그 존재를 부정했다고 합니다.
무리수의 사칙연산
반면 무리수를 한 번 볼까요?
무리수 + 무리수는 무리수일까요?
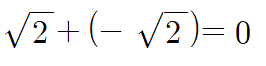
아님을 바로 알 수 있죠.
다른 사칙 연산은 어떨까요?

무리수끼리 연산했는데 유리수가 나오는군요.
즉, 무리수는 모든 연산에 대해서
닫혀있지 않네요.
그렇다면 무리수 + 무리수는 유리수일까요?

이런.. 그렇다면 무리수와 무리수는
어떤 사칙연산을 했을 때 그 결과가
유리수다, 혹은 무리수다 하고
결론을 내릴 수 없습니다.
함수의 수렴과 발산
이러한 관계가 함수에서 수렴/발산을 판정할 때도
동일하게 사용될 수 있습니다.

즉, 수렴하는 함수집합과 사칙연산은
닫혀있는 관계죠.
반대로 발산하는 함수집합과 사칙연산은
닫혀있지 않습니다.
여기서 닫혀있지 않다는 건,
결과를 보장할 수 없다는 거에요.
발산하는 함수끼리 연산했을 때는
발산하는 함수가 나오기도 하고,
수렴하는 함수가 나오기도 합니다.
위에서 무리수의 연산과 비슷하다고
생각하시면 돼요.
언제는 유리수가 나오고 언제는 무리수가 나오듯이-
그래서 연속/불연속을 판정할 때
이 성질을 이용하면 쉽게 판정이 됩니다.
다음에 예시를 들어서 좀 더 자세히 써볼게요:-)
함수의 연속과 불연속
마찬가지로 연속하는 함수집합과
사칙연산도 닫혀있습니다.
연속하는 함수끼리 사칙연산을 시행해도
결과는 항상 연속입니다.

불연속하는 함수끼리는
연속이 나올 때도 있고 불연속일 때도 있어서
뭐다!!라고 이야기 할 수 없죠.
| 닫혀있다. | 닫혀있지 않다. | |
| 유리수 vs 무리수 | 유리수 + 유리수 = 유리수 | 무리수 + 무리수 = ?? |
| 유리수 - 유리수 = 유리수 | 무리수 - 무리수 = ?? | |
| 유리수 x 유리수 = 유리수 | 무리수 x 무리수 = ?? | |
| 유리수 / 유리수( 0이 아님 ) = 유리수 | 무리수 / 무리수 = ?? | |
| 수렴 vs 발산 | 수렴 + 수렴 = 수렴 | 발산 + 발산 = ?? |
| 수렴 - 수렴 = 수렴 | 발산 - 발산 = ?? | |
| 수렴 x 수렴 = 수렴 | 발산 x 발산 = ?? | |
| 수렴 / 수렴( 0이 아님) = 수렴 | 발산 / 발산( 0이 아님) = ?? | |
| 연속 vs 불연속 | 연속 + 연속 = 연속 | 불연속 + 불연속 = ?? |
| 연속 - 연속 = 연속 | 불연속 - 불연속 = ?? | |
| 연속 x 연속 = 연속 | 불연속 x 불연속 = ?? | |
| 연속 / 연속( 0이 아님) = 연속 | 불연속 / 불연속( 0이 아님) = ?? |
연산에 대하여 닫혀있다는 개념이
제가 고1때는 배웠는데 꽤 오래 전 삭제 됐습니다.
알아두면 유용한 개념이기에,
가볍게 훑어보시면 좋을 것 같네요.
그럼 열공하셔요~!
'고등수학 (2015 개정 교육과정) > 수학2' 카테고리의 다른 글
| 삼차함수 접선의 개수 (2) | 2021.07.18 |
|---|---|
| [함수의 연속] 연속 x 불연속 문제 (0) | 2021.04.22 |
| 합성함수의 극한값 (3) | 2020.12.02 |
| [수학 발표 추천 주제] 함수의 연속 : 모든 점에서 불연속인 함수 (디리클레 함수) (10) | 2020.11.24 |
| [가우스] 가우스의 기본 성질 (0) | 2020.02.15 |