오늘은 위치에 따라
삼차함수에 그을 수 있는
접선의 개수에 대해 정리해봅시다.

삼차함수의 접선의 개수는
교육과정에 있는 내용은 아닙니다.
그렇지만,
모의고사 등에 꾸준히 나오고,
내신에서 이 내용을 아느냐/모르느냐에 따라
시간 차이가 많이 나기 때문에
꼭 알아두는게 좋습니다.
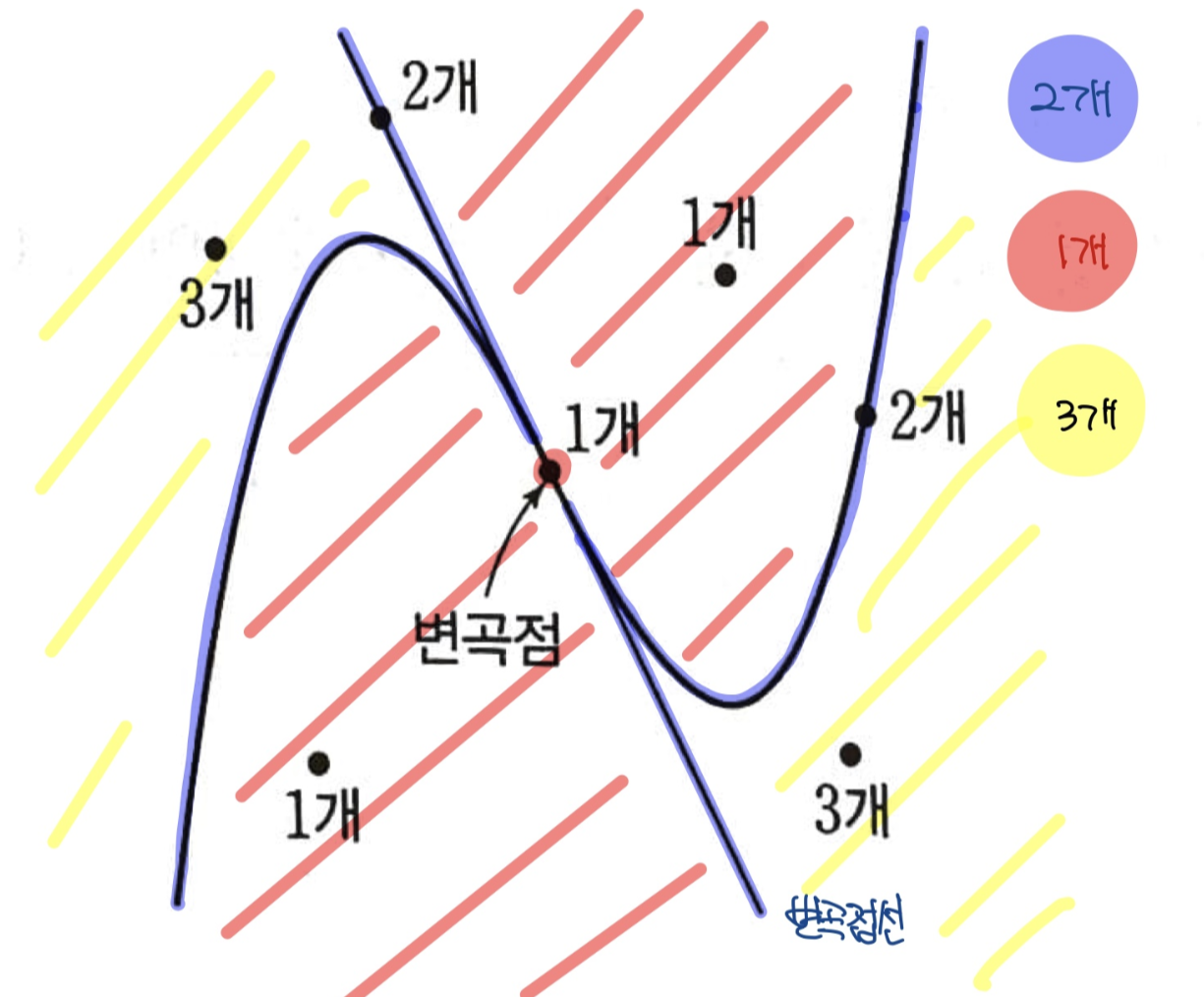
접선의 개수를 구할 때는,
삼차함수의 그래프와 변곡점에서의 접선
이 두 가지는 경계로 그려놓고 판단하시면 됩니다.
변곡점이란?
변곡점이라는 용어 자체가 미적분에서 나와서
문과 학생들에게는 좀 생소한 용어죠.
간단하게 설명하자면,
그래프의 오목/볼록이 바뀌는 점입니다.
위로 볼록인 상태에서
아래로 볼록인 상태로 변하거나,
아래로 볼록인 상태에서
위로 볼록인 상태로 변하는 점이죠.
구하는 방법은 삼차함수에서는
두 번 미분해서 0되는 점을 찾으시면 됩니다.!
변곡점에 대한 좀 더 상세한 건
이계도함수를 이용해서 설명해야 하므로,
문과는 딱 여기까지만 아셔도 됩니다.
나중에 추가로 포스팅할게요 :-)
아무튼 우선은 각 위치에 따른 접선을 다 그려볼게요.!
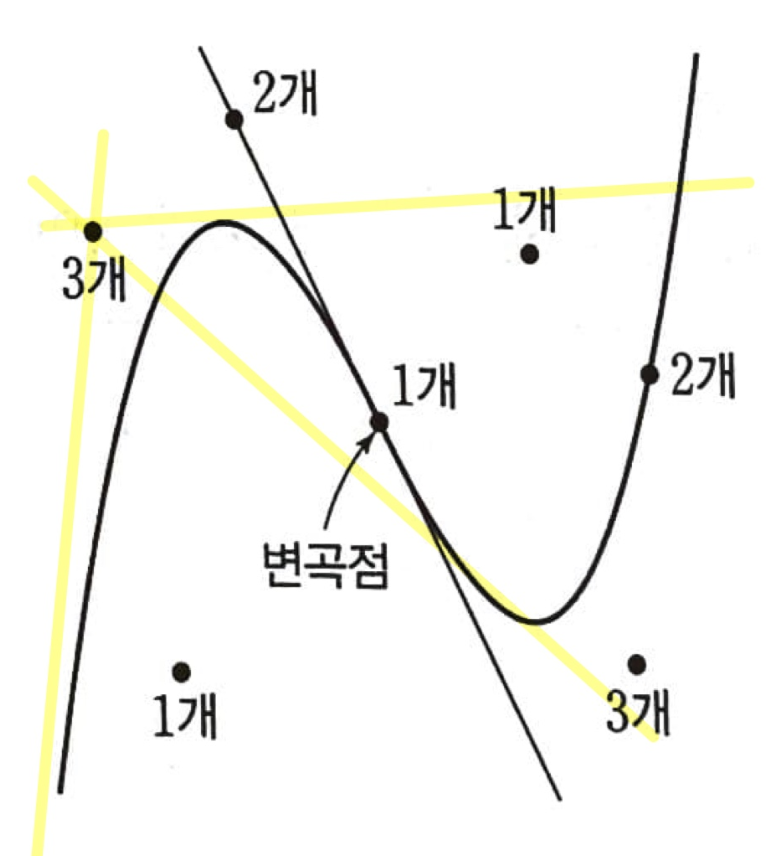
1. 접선이 3개인 경우
: 곡선과 변곡점 바깥에서 그은 접선은
그림과 같이 3개가 나옵니다.

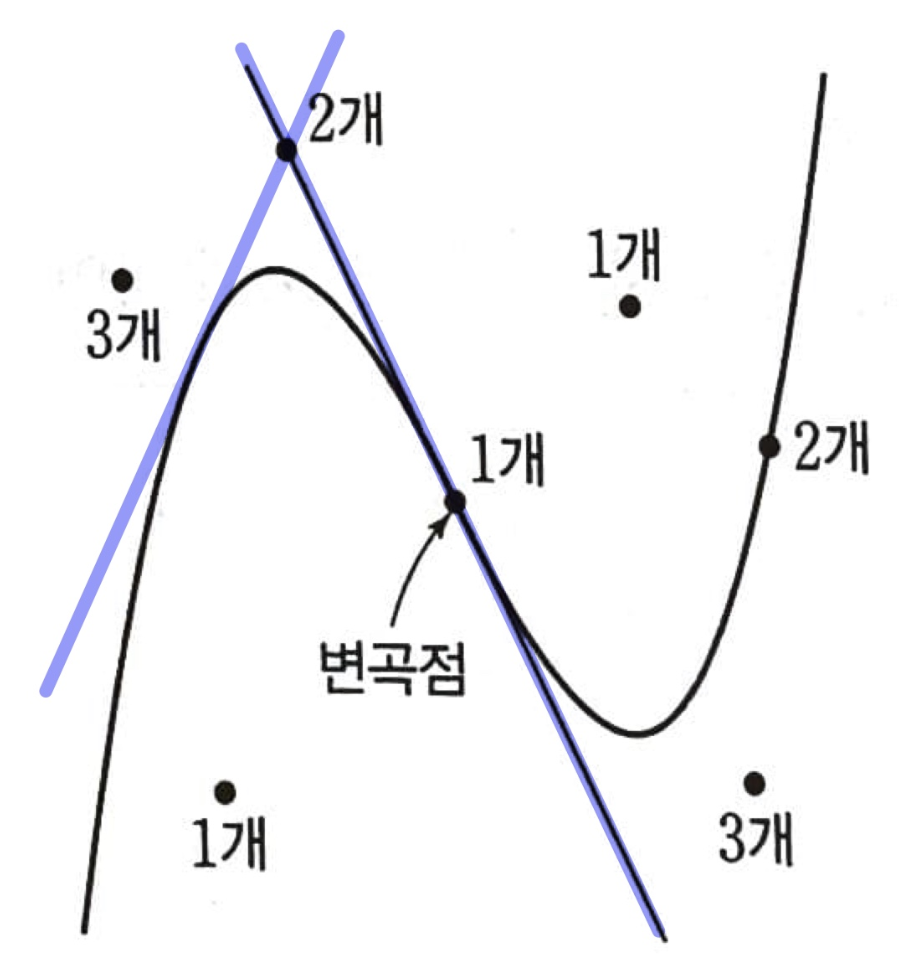
2. 접선이 2개인 경우
: 변곡점을 제외하고
함수 위에 있는 경우와,
변곡점에서의 접선 위에 있는 경우는
접선이 2개씩 나옵니다.

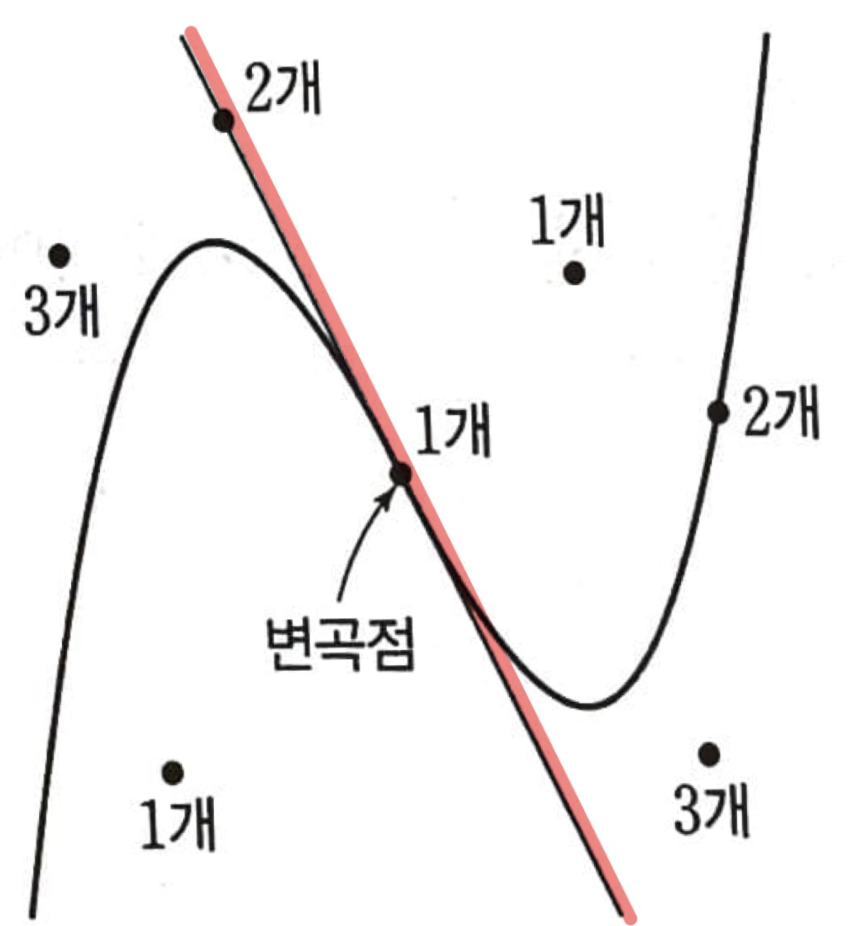
3. 접선이 1개인 경우
: 함수에서 오목한 부분에 있는 점과
변곡점에서의 접선은 1개만 있습니다.


삼차함수에서의 접선의 개수는
이 내용을 모르는 경우에는
계산이 매우 복잡하므로,
보통 문제에서 축에 평행한 직선으로 줍니다.
그렇지만 이 내용을 안다면
더 간단하게 풀 수 있죠.
이론은 알겠는데,
그래서 실제로 문제를 어떻게 푸는지
궁금하신 분들은,
문제풀이 포스팅 완료했으니
같이 보시면 도움이 될 거에요!
https://ladyang86.tistory.com/189
삼차함수 접선의 개수 문제 모음
이전에 포스팅했던 삼차함수 접선의 개수 문제 모아보았습니다. 방정식으로 풀기보다는 그래프의 특성을 이용하여 푸는 편이 훨씬 빠르답니다. 혹시 이론이 기억이 안 나신다면, 기본적인 내용
ladyang86.tistory.com
'고등수학 (2015 개정 교육과정) > 수학2' 카테고리의 다른 글
| 함수의 극한 진위판정(참/거짓) 문제 (6) | 2021.08.21 |
|---|---|
| 미분계수 공식 정리 (h 등장하는 꼴일 때) (0) | 2021.07.24 |
| [함수의 연속] 연속 x 불연속 문제 (0) | 2021.04.22 |
| 합성함수의 극한값 (3) | 2020.12.02 |
| [수학 발표 추천 주제] 함수의 연속 : 모든 점에서 불연속인 함수 (디리클레 함수) (10) | 2020.11.24 |