오늘은 복이차식 인수분해를
풀어볼거에요.

복이차식에서 '복'자란
겹칠 복자입니다.
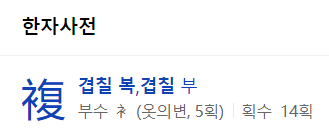
복부호동순이란 말도 들어보셨죠?
같은 한자를 씁니다.
±와 같이 부호를 겹쳐서 쓴 걸
복부호라고 읽는데,
동순은 순서가 같단 뜻이에요.
겹쳐진 부호끼리 순서가 같은 거죠.
위에 있는 부호끼리 한쌍,
아래 있는 부호끼리 한쌍
뭐 이렇게 보시면 됩니다.
아무튼 복이차식은
말 그대로 풀자면
이차식이 겹쳐져 있는(?) 형태입니다.

x대신 x^2을 넣는다면
복이차식이 되죠.
서론이 길었네요.
본격적으로 인수분해 해봅시다.!
우선 복이차식 형태를 본다면
가장 먼저 치환을 해서
인수분해를 시도해봅니다.
그런데 만약 안된다?
이럴 때 오늘 배운 합차꼴로
인수분해 하시면 됩니다.

합차꼴로 변형할 때의 핵심은
완전 제곱식 두 개를
만들어 주는 것이에요.
보통은 이차항을 적절히 쪼개서
완전 제곱식을 만들어 줍니다.
그럼 예제를 한 번 풀어볼까요?
문제1

이차항을 적절히 쪼개서
합차꼴로 만들어 풉니다.
사실 이건 답지를 보면 쉽습니다.
처음부터 만들어 나가는게 어렵죠.
결국 핵심은
이차항을 도대체 어떻게 쪼개느냐?-겠죠?
이럴 때는 4차항과 상수항에 집중해서
먼저 완전 제곱식을 만들어봅니다.

그리고 가운데 부호가
뭐가 들어갈지를 생각해보세요.
둘 중 합차꼴로 자연스럽게 변형되는 걸
채택하시면 됩니다.
한번 더 해볼까요?
문제2

뭘로 쪼갤지 보이지 않는다면,
상수항과 4차항에 집중해보세요.
뭘 제곱하면 저런 항이 나올까?
를 역으로 생각해보시면 됩니다.

가운데 부호에 따라 다르게 쪼개질테니,
둘 다 해보시고 합차꼴이 나오는 걸
선택해주시면 됩니다.

아래 두 문제 정도 더 풀어두었으니,
연습해보면서 감을 익혀보도록 해요.
이차항이 잘 나뉘어지는가?
-에 집중하면서 푸시면 됩니다.
문제3

문제4

고등학교부터는 인수분해만 하더라도
방법이 굉장히 많기 때문에,
어떤 식을 봤을 때,
어떻게 인수분해 할지
머릿속으로 잘 고민하셔야 해요.
기본적으로 훈련이 잘 되어있어야겠죠?
힘내서 연습합시다! ^^
'고등수학 (2015 개정 교육과정) > 고등수학(상)' 카테고리의 다른 글
| 계수가 대칭인 상반방정식 (대칭형 사차방정식) 푸는 방법 (0) | 2021.05.08 |
|---|---|
| 곱셈공식, 인수분해 - 문자 세 개인 경우 총 정리 (0) | 2021.04.01 |
| 곱셈공식의 변형 - (문자가 2개인 경우, 거듭제곱) (0) | 2021.03.05 |
| 삼각형 무게중심 성질 (m:n 내분점의 무게중심, 거리 제곱의 합) (0) | 2021.02.13 |
| 정수조건 부정방정식의 해 (인수분해 형태로 바꾸기) (0) | 2020.11.21 |