한량 지아이의 수학 LIFE

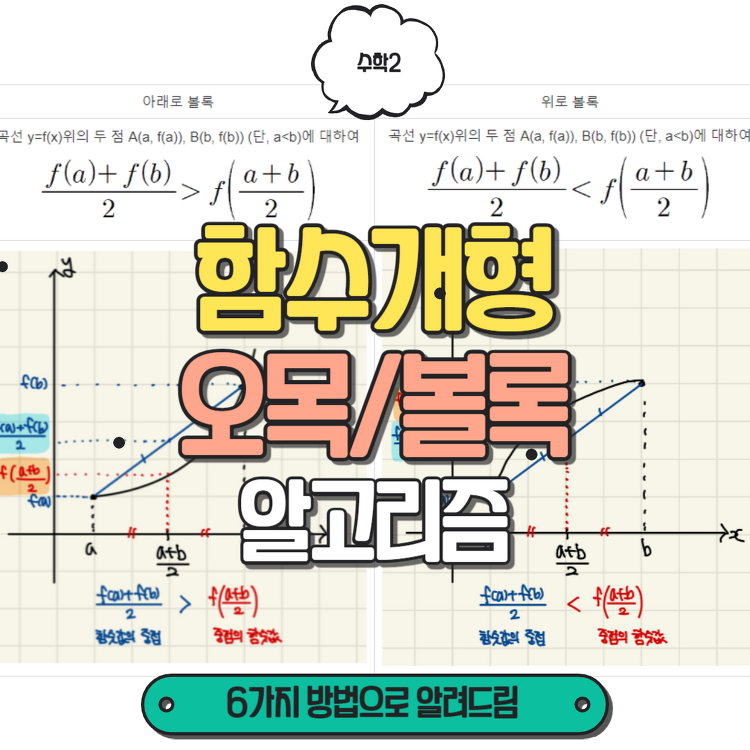
정적분의 넓이 공식을 배운 제자가,삼차함수와 접선이 만나는 넓이 공식을 좀 더 연습하고 싶다고 요청하여 문제 업로드 합니다.  세 근이 1, 1, -2이므로 근의 차는 3따라서 공식을 사용하면 81/12 = 27/4정답 : 27/4 세 근이 0. 0, 3 이므로 근의 차는 3따라서 공식을 사용하면 81/12 = 27/4정답 : 27/4세 근이 -3, -3, 3이므로 근의 차는 6공식을 사용하면 1296/12 = 108정답 : 108세 근이 t, t, -2t 이므로 근의 차는 4t공식을 사용하면 (256t^4)/12 = 4/3이므로 t=2 만약 이 공식을 모른다면?  [필수암기] 정적분 넓이 공식 (이차함수, 삼차함수 접선)정적분 넓이 공식 (이차함수 근, 삼차함수 중근) 오늘은 굉장히 자주 사용되지만, ..

이제부터는 한 문제씩이라도 문제 풀이를 같이 올려볼까 합니다. 한 번에 모아서 올리려니 양이 많아서 계속 미루게 되네요. -ㅅ-; 그래야 뭐 나중에 풀이를 추가하거나, 강의를 찍거나 할 수도 있을 것 같아요.  2022년 시행 2023 수능 #22번입니다.객관식 마지막 번호로, 해석이 상당히 어렵고,그래프를 그린 이후에 식 세워서 답을 찾는 과정까지도 다 해보셔야 합니다.먼저 문제 (가)조건을 봤을 때  f'(x)가 최고차항의 계수가 3인 이차함수라는 것 말고는, 당장은 뭘 더 할 수 있는게 없으니 (나)조건도 살펴보죠.   이제 그래프는 다 완료가 되었군요. 식을 세워서 마무리까지 해봅시다.저는 평소에 접선을 이용해서 식을 세우는 편이라 이대로 해봤는데 계수가 분수가 나와서 약간의 짜증이..올라오더군요..

2022년 시행된 6월 모의고사 질문을 받았습니다. 학생이 해설지가 잘 이해가 안 된다고 갖고 왔는데, 저도 해설지 보다 혈압 올라서 작성하는 포스팅입니다. 저는 적분은 '함수값을 쌓는다'라고 표현을 합니다. 점이 쌓이면 선이 되고, 선이 쌓이면 면이 되듯이, 함숫값을 쌓으면 면적이 되죠. 이걸 이용하여 간단한 문제를 먼저 풀어볼게요.  예제아래 그림은 이차함수 y=f(x)의 그래프이다. 함수 g(x)를로 정의할 때, 함수 g(x)의 최솟값은?정답 : g(2)음수인 면적을 가장 많이 포함해야 하므로,g(2)가 됩니다. 2023년 6월 20번최고차항의 계수가 2인 이차함수 f(x)에 대하여 함수는 x=1과 x=4에서 극소이다. f(0)의 값을 구하시오. 주어진 조건으로부터f(x)가 어떻게 생겼을지를 고민해..

미분계수 식변형 연습문제입니다. 알고리즘 1. 우선은 f안에 미지수가 들어있는 식을 가장 앞에 씁니다. 2. 어떤 상수가 들어가면 좋을지를 판단합니다. 3. 만약 f(x)앞에 다른 무언가가 붙어있다면 그걸 같이 곱해서 빼고 더해줍니다. 멀쩡한 식에 갑자기 분자에서 무언가를 빼기만 할 순 없겠죠? 방금 뺀 수를 부호만 바꾸어서 더해줍니다. 그러면 식이 잘 분해가 되어서 정리가 된답니다 :-) 예제 정답 : 2 문제 정답 : (1) af'(a)-f(a) (2) 2af(a)-a^2f'(a) (3) 3a^2f(a)-a^3f(a) (4) 2af(a)+a^2f'(a) 제가 손목 회복이 더디게 되고 있는 관계로 풀이는 추후 업로드 하고 우선 문제와 정답만 업로드합니다. 문제나 풀이는 추가 될 수도 있습니다.

내신 문제들을 풀면서, 적분 속도 문제 중 괜찮은 문제들을 몇 문제 실어보았습니다. 한 번에 안 풀리거나 조금 생소한 문제들이 있을 수도 있어요. :-) 완벽한 포스팅을 지향하다가 시기를 놓칠 수도 있을것 같아 우선 문제와 정답부터 업로드하고 풀이는 차차 업데이트 예정입니다. 문제1 수직선 위를 움직이는 점 P의 시각 t에서의 속도 v(t)의 그래프는 아래 그림과 같다. t=1, t=6일 때의 점 P의 위치가 각각 1, 5/2일 때, t=8일 때의 점 P의 위치를 구하는 풀이과정과 답을 서술하시오. (단, a>0) 정답 : 9/2 * 초기 위치 안 준 문제라 처음에 a값을 잘못 구해서 헤맬 수 있음. 문제2 지아이는 교내대회에 대비하여 다음의 수리논술 예상 문제를 풀고 있다. 수리논술 예상 문제 직선 도..

삼차함수 그래프를 배우다 보면, 서로 다른 세 실근/두 실근을 갖는다는 조건을 극댓값x극솟값의 부호로 푸는 설명을 볼 수 있습니다. 학습하면서 접하는 꽤 많은 문제가 굳이 극댓값x극솟값까지 구하지 않아도, 간단하게 인수분해가 되는 유형도 있어요. 그렇지만 오늘은 극댓값x극솟값으로 곱했을 때 더 쉬운 문제들을 풀어볼게요. 예제 2020년 10월학평 나형 #28 먼저 주어진 함수를 미분해서 개형을 그립니다. 문제

직선을 제외한 곡선 함수는 평면에서 위로 볼록하거나, 아래로 볼록하거나 둘 중 하나입니다. 그런데 보통 문제에서 f(x)는 어느 구간에서 위로 볼록하다- 이런식으로 주지 않거든요. 이걸 수식으로 어떻게 나타내는지 오늘 살펴볼 거에요. 1. 고1 수학 : 내분점과 함숫값의 내분점을 비교. (주로 중점을 사용) 아래로 볼록 위로 볼록 곡선 y=f(x)위의 두 점 A(a, f(a)), B(b, f(b)) (단, a

이전에 포스팅했던 삼차함수 접선의 개수 문제 모아보았습니다.방정식으로 풀기보다는 그래프의 특성을 이용하여 푸는 편이 훨씬 빠르답니다. 혹시 이론이 기억이 안 나신다면, 기본적인 내용은 아래 포스팅을 참고하시고, 오늘은 문제만 그래프 그려서 빠르게 풀어볼게요. https://ladyang86.tistory.com/109 삼차함수 접선의 개수오늘은 위치에 따라 삼차함수에 그을 수 있는 접선의 개수에 대해 정리해봅시다. 삼차함수의 접선의 개수는 교육과정에 있는 내용은 아닙니다. 그렇지만, 모의고사 등에 꾸준히 나오고, 내신에ladyang86.tistory.com 문제12024 수능완성 2회 22번문제22015년 10월학평 A형 29번  문제3쎈 수학2 #417문제42019-2-2-f 대전외고 #19정답 : 6..

오늘은 가우스 기호가 들어있는 함수의 극한 문제를 조금 풀어볼게요. '선생님, 가우스 시험에 나와요?' 라고 물어본다면, 대답하기가 조금 애매합니다. 뭐, 교육과정에서 필수로 꼭 들어있는 내용은 아니지만, [x]는 x 이하의 정수라는 뜻을 주면, 솔직히 해석을 못할 정도로 어렵지도 않거든요.. 가우스 함수의 성질 정리는 나중에 기회가 되면 하고, 오늘은 문제 위주로 풀도록 하겠습니다. 문제 1 문제2 다음 중 그 값이 가장 큰 것은? (단, [x]는 x 이하의 최대 정수) 문제3 문제4 오늘 실은 문제는 기본 극한뿐이지만, 나중에는 아래와 같이 조임정리를 쓰는 가우스 들어간 극한 문제도 추가할게요!

기본적인 롤의 정리, 평균값 정리 문제 정도는 풀지만,뭔가 내가 이걸 잘 아는 것 같지는 않고,연습을 좀 더 해보고 싶은데 더 뭔가 어려운 문제는 없을까..? 하는 고민을 학생을 위한 오늘의 포스팅입니다.평균값 정리함수 f(x)가 [a,b]에서 연속이고 (a,b)에서 미분 가능할 때,(a, f(a)), (b,f(b))의 평균변화율 = f'(c)인 c가(a,b) 사이에 적어도 하나 존재한다. 해설..은 작성 중이라, 차차 업데이트 할게요! 우선 문제부터 올리겠습니다.^^문제 1정답 : 9 문제 2다항함수 f(x)에 대하여 f(1)=1, f(3)=2, f(4)=7일 때,에서 옳은 것을 고르시오. 문제3정답 : 12문제 4241010 추가문제출처 2020 수능특강 Ch4 Lv3. #2정답 : 15/2(나),(..